Question

已知函数．
（1）求函数f（x）的单调区间和极值；
（2）求证：当x＞1时，f（x）＞g（x）；
（3）如果x₁≠x₂，且f（x₁）=f（x₂），求证：f（x₁）＞f（2-x₂）．

Answer 1

解：（1）∵f（x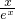）=，∴f'（x）=．
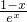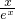令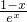f'（x）=0，解得x=1．

x	（-∞，1）	1	（1，+∞）
f'（x）	+	0	-
f（x）	↗	极大值	↘

∴f（x）在（-∞，1）内是增函数，在（1，+∞）内是减函数，
∴当x=1时，f（x）取得极大值f（1）=．

（2）证明：令F（x）=f（x）-g（x）=，
则F'（x）=．
当x＞1时，1-x＜0，2x＞2，从而e²-e^2x＜0，
∴F'（x）＞0，F（x）在（1，+∞）是增函数．
∴F（x）＞F（1）==0，故当x＞1时，f（x）＞g（x）．
（3）证明：∵f（x）在（-∞，1）内是增函数，在（1，+∞）内是减函数、
∴当x₁≠x₂，且f（x₁）=f（x₂）时，x₁、x₂不可能在同一单调区间内．
不妨设x₁＜1＜x₂，
由（2）的结论知x＞1时，F（x）=f（x）-g（x）＞0，∴f（x₂）＞g（x₂）．
∵f（x₁）=f（x₂），∴f（x₁）＞g（x₂）．
又g（x₂）=f（2-x₂），∴f（x₁）＞f（2-x₂）．
分析：（1）对f（x）求导，令f′（x）=0，解出后判断根的两侧导函数的符号即可确定出单调性和极值．（2）比较两个函数的大小可将它们作差，研究新函数的最小值，使最小值大于零，不等式即可证得．（3）由（2）的结论知x＞1时，F（x）=f（x）-g（x）＞0，∴f（x₂）＞g（x₂）．∵f（x₁）=f（x₂），∴f（x₁）＞g（x₂）．即可证得结论．
点评：此题是个难题．主要考查函数与导数的综合应用能力，具体涉及到用导数来研究函数的单调性、极值等基础知识，考查运算能力及用函数思想分析解决问题的能力．