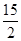题目内容
(本小题满分14分)已知函数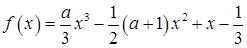 (
(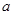
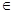 R).
R).
(1)若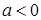 ,求函数
,求函数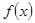 的极值;
的极值;
(2)是否存在实数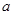 使得函数
使得函数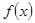 在区间
在区间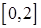 上有两个零点,若存在,求出
上有两个零点,若存在,求出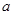 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
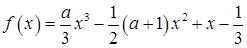 (
(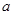
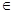 R).
R).(1)若
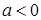 ,求函数
,求函数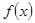 的极值;
的极值;(2)是否存在实数
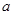 使得函数
使得函数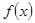 在区间
在区间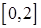 上有两个零点,若存在,求出
上有两个零点,若存在,求出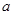 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(1) ,
,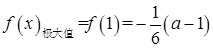 (2)存在实数
(2)存在实数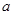 ,当
,当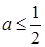 时,函数
时,函数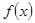 在区间
在区间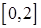 上有两个零点
上有两个零点
 ,
,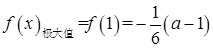 (2)存在实数
(2)存在实数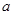 ,当
,当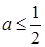 时,函数
时,函数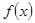 在区间
在区间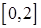 上有两个零点
上有两个零点试题分析:解:(1)
 ………………2分
………………2分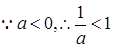 ,
,| | 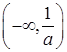 | 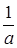 | 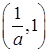 | 1 | 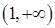 |
 | - | 0 | + | 0 | - |
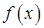 | 递减 | 极小值 | 递增 | 极大值 | 递减 |
 ,
,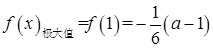 ……6分
……6分(2)
 ,
,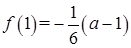
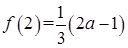 ,
, 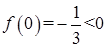 ……………8分
……………8分① 当
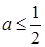 时,
时,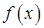 在
在 上为增函数,在
上为增函数,在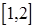 上为减函数,
上为减函数,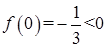 ,
, ,
, ,所以
,所以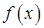 在区间
在区间 ,
, 上各有一个零点,即在
上各有一个零点,即在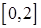 上有两个零点; ………………………10分
上有两个零点; ………………………10分当
 时,
时,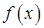 在
在 上为增函数,在
上为增函数,在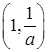 上为减函数,
上为减函数,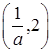 上为增函数,
上为增函数,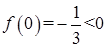 ,
, ,
, ,
,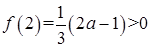 ,所以
,所以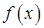 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在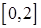 上只有一个零点; ………………………12分
上只有一个零点; ………………………12分③ 当
 时,
时,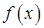 在
在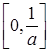 上为增函数,在
上为增函数,在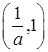 上为减函数,
上为减函数, 上为增函数,
上为增函数,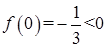 ,
, ,
, ,
,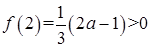 , 所以
, 所以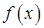 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在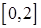 上只有一个零点; …………………………13分
上只有一个零点; …………………………13分故存在实数
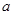 ,当
,当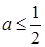 时,函数
时,函数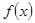 在区间
在区间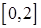 上有两个零点…………………14分
上有两个零点…………………14分点评:主要考查了导数在研究函数中的运用,利用导数符号判定单调区间,同时根据极值的正负来确定零点,属于常规试题。中档题。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
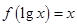 ,则
,则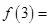 ( )
( )


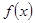 的定义域为实数集R,
的定义域为实数集R,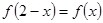 ,且当
,且当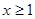 时,
时,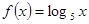 ,则有( )
,则有( )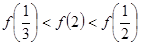
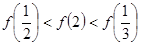
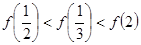
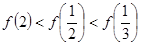
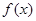 是定义在R上的函数且
是定义在R上的函数且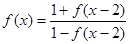 ,且
,且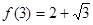 ,则
,则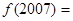

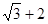
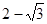
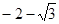
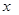 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为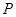 元,且
元,且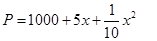 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为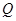 元,其中
元,其中
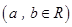 ,
,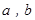 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)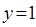 与
与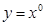
 与
与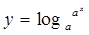
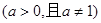
 与
与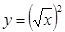
 与
与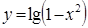
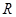 的函数
的函数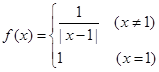 ,若函数
,若函数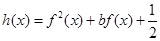 有
有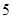 个不同的零点
个不同的零点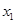 ,
,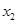 ,
,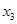 ,
,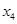 ,
,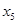 ,则
,则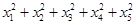 等于_______________
等于_______________  、
、 之间的“理想距离”为:
之间的“理想距离”为: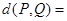
 ;若
;若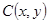 到点
到点 、
、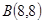 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数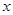 、
、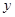 满足
满足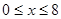 、
、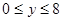 ,则所有满足条件的点
,则所有满足条件的点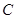 的轨迹的长度之和是
的轨迹的长度之和是