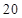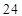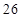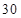题目内容
在等差数列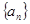 和等比数列
和等比数列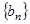 中,
中,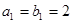 ,
,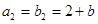 ,
,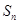 是
是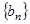 前
前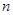 项和.
项和.
(1)若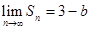 ,求实数
,求实数 的值;
的值;
(2)是否存在正整数 ,使得数列
,使得数列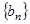 的所有项都在数列
的所有项都在数列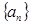 中?若存在,求出所有的
中?若存在,求出所有的 ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数 ,使得数列
,使得数列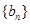 中至少有三项在数列
中至少有三项在数列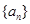 中,但
中,但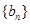 中的项不都在数列
中的项不都在数列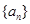 中?若存在,求出一个可能的
中?若存在,求出一个可能的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
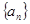 和等比数列
和等比数列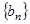 中,
中,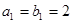 ,
,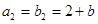 ,
,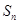 是
是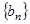 前
前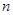 项和.
项和.(1)若
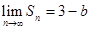 ,求实数
,求实数 的值;
的值;(2)是否存在正整数
 ,使得数列
,使得数列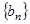 的所有项都在数列
的所有项都在数列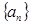 中?若存在,求出所有的
中?若存在,求出所有的 ,若不存在,说明理由;
,若不存在,说明理由;(3)是否存在正实数
 ,使得数列
,使得数列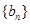 中至少有三项在数列
中至少有三项在数列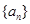 中,但
中,但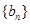 中的项不都在数列
中的项不都在数列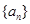 中?若存在,求出一个可能的
中?若存在,求出一个可能的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)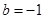 ;(2)存在,
;(2)存在, ;(3)存在,
;(3)存在,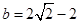 (答案不唯一).
(答案不唯一).
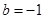 ;(2)存在,
;(2)存在, ;(3)存在,
;(3)存在,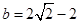 (答案不唯一).
(答案不唯一).试题分析:(1)数列
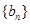 是等比数列,其前
是等比数列,其前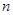 和的极限存在,因此有公式
和的极限存在,因此有公式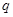 满足
满足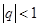 ,且极限为
,且极限为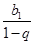 ;(2)由于
;(2)由于 是正整数,因此可对
是正整数,因此可对 按奇偶来分类讨论,因此当
按奇偶来分类讨论,因此当 为奇数时,等比数列
为奇数时,等比数列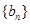 的公比不是整数,是分数,从而数列
的公比不是整数,是分数,从而数列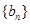 从第三项开始每一项都不是整数,都不在数列
从第三项开始每一项都不是整数,都不在数列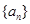 中,而当
中,而当 为偶数时,数列
为偶数时,数列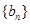 的所有项都在
的所有项都在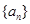 中,设
中,设 ,则
,则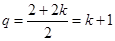 ,
,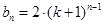 展开有
展开有
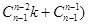
 ,这里用到了二项式定理,
,这里用到了二项式定理,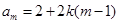 ,结论为真;(3)存在时只要找一个
,结论为真;(3)存在时只要找一个 ,首先
,首先 不能为整数,下面我们只要写两数列的通项公式,让
不能为整数,下面我们只要写两数列的通项公式,让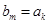
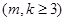 ,取特殊值求出
,取特殊值求出 ,如取
,如取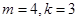 ,可得
,可得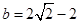 ,此时
,此时 在数列
在数列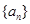 中,由于
中,由于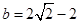 是无理数,会发现数列
是无理数,会发现数列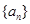 除第一项以外都是无理数,而
除第一项以外都是无理数,而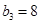 是整数,不在数列
是整数,不在数列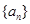 中,命题得证,(如取其它的
中,命题得证,(如取其它的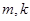 又可得到另外的
又可得到另外的 值).
值).试题解析:(1)对等比数列
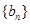 ,公比
,公比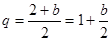 .
.因为
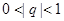 ,所以
,所以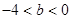 . 2分
. 2分解方程
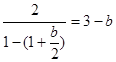 , 4分
, 4分得
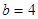 或
或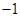 .
. 因为
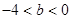 ,所以
,所以 . 6分
. 6分(2)当
 取偶数
取偶数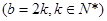 时,
时,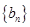 中所有项都是
中所有项都是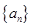 中的项. 8分
中的项. 8分证: 由题意:
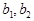 均在数列
均在数列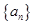 中,
中,当
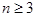 时,
时,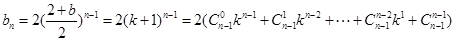
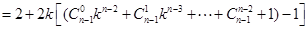
说明
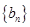 的第n项是
的第n项是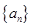 中的第
中的第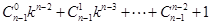 项. 10分
项. 10分当
 取奇数
取奇数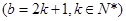 时,因为
时,因为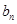 不是整数,
不是整数,所以数列
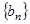 的所有项都不在数列
的所有项都不在数列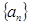 中。 12分
中。 12分综上,所有的符合题意的
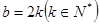 。
。(3)由题意,因为
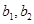 在
在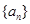 中,所以
中,所以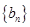 中至少存在一项
中至少存在一项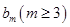 在
在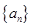 中,另一项
中,另一项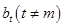 不在
不在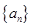 中。 14分
中。 14分由
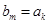 得
得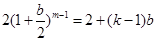 ,
,取
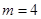 得
得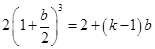 ,即
,即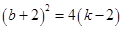 .
.取
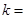 4,得
4,得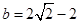 (舍负值)。此时
(舍负值)。此时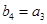 。 16分
。 16分当
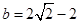 时,
时,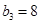 ,
,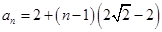 ,对任意
,对任意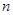 ,
, . 18分
. 18分综上,取
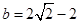 .
.(此问答案不唯一,请参照给分)

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
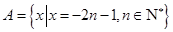 ,
,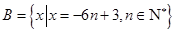 ,设
,设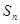 是等差数列
是等差数列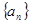 的前
的前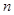 项和,若
项和,若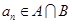 ,且首项
,且首项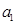 是
是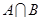 中的最大数,
中的最大数, 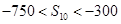 .
.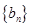 满足
满足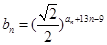 ,求
,求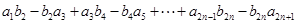 的值.
的值.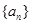 满足:当
满足:当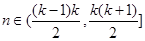 (
(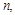
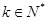 )时,
)时,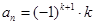 ,
,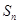 是数列
是数列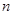 项和,定义集合
项和,定义集合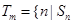 是
是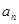 的整数倍,
的整数倍,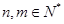 ,且
,且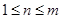
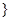 ,
,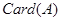 表示集合
表示集合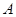 中元素的个数,则
中元素的个数,则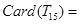 ,
,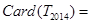 .
.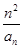 ,证明:bn≤
,证明:bn≤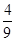 .
.
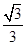
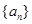 ,
,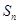 为其前
为其前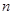 项和,若
项和,若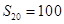 ,且
,且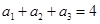 ,则
,则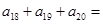 ( )
( )