题目内容
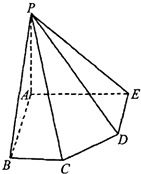
 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2| 2 |
(1)求证:PA⊥平面ABCDE;
(2)若G为PE中点,求证:AG⊥平面PDE
(3)求二面角A-PD-E的正弦值;
(4)求点C到平面PDE的距离.
分析:(1)欲证PA⊥平面ABCDE,只需证明PA垂直平面ABCDE上的两条相交直线即可,在三角形PAB中运用勾股定理,可证明PA垂直于AB,在三角形PAE中,同样用勾股定理,可证明PA垂直AE,这样就可证明PA⊥平面ABCDE.
(2)欲证AG⊥平面PDE,只需证明AG垂直于平面PDE中的两条相交直线,在三角形中PA=AE=2a,所以可知AG垂直PE,再通过
ED⊥平面PAE,利用线面垂直的性质,可得AG垂直于DE,则AG⊥平面PDE可证.
(3)欲求二面角A-PD-E的大小,先找到二面角的平面角,利用三垂线定理,因为AG⊥平面PDE,所以只需过G作GH⊥PD于H,连AH,则AH⊥PD,∴∠AHG为二面角A-PD-E的平面角.再放入直角△PAE中,求出∠AHG的正弦值.
(4)欲求点C到平面PDE的距离,只需过C点向平面PDE作垂线,但是垂足位置不容易找到,所以可以转化为其它点到平面的距离.证明CF∥DE,则点C到平面PDE的距离等于F到平面PDE的距离,就可求F到平面PDE的距离.再由(3)中结论知FG⊥平面PDE,所以FG的长即F点到平面PDE的距离,放入△PAE中求出即可.
(2)欲证AG⊥平面PDE,只需证明AG垂直于平面PDE中的两条相交直线,在三角形中PA=AE=2a,所以可知AG垂直PE,再通过
ED⊥平面PAE,利用线面垂直的性质,可得AG垂直于DE,则AG⊥平面PDE可证.
(3)欲求二面角A-PD-E的大小,先找到二面角的平面角,利用三垂线定理,因为AG⊥平面PDE,所以只需过G作GH⊥PD于H,连AH,则AH⊥PD,∴∠AHG为二面角A-PD-E的平面角.再放入直角△PAE中,求出∠AHG的正弦值.
(4)欲求点C到平面PDE的距离,只需过C点向平面PDE作垂线,但是垂足位置不容易找到,所以可以转化为其它点到平面的距离.证明CF∥DE,则点C到平面PDE的距离等于F到平面PDE的距离,就可求F到平面PDE的距离.再由(3)中结论知FG⊥平面PDE,所以FG的长即F点到平面PDE的距离,放入△PAE中求出即可.
解答:解:(1)证明∵PA=AB=2a,PB=2
a,∴PA2+AB2=PB2,∴∠PAB=90°,
即PA⊥AB.同理PA⊥AE.∵AB∩AE=A,∴PA⊥平面ABCDE.
(2)∵∠AED=90°,∴AE⊥ED.∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE,所以DE⊥AG.
∵PA=AE,G为PE中点,所以AG⊥PE,∴AG⊥平面PDE
(3)∵∠AED=90°,∴AE⊥ED.∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE.过A作AG⊥PE于G,过DE⊥AG,
∴AG⊥平面PDE.过G作GH⊥PD于H,连AH,由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角.
在直角△PAE中,AG=
a.在直角△PAD中,AH=
a,∴在直角△AHG中,sin∠AHG=
=
.
∴二面角A-PD-E的正弦值为
.
(4)∵∠EAB=∠ABC=∠DEA=90°,BC=DE=a,AB=AE=2a,取AE中点F,连CF,∵AF∥=BC,∴四边形ABCF为平行四边形.∴CF∥AB,而AB∥DE,∴CF∥DE,而DE?平面PDE,CF?平面PDE,∴CF∥平面PDE.∴点C到平面PDE的距离等于F到平面PDE的距离.∵PA⊥平面ABCDE,∴PA⊥DE.又∵DE⊥AE,∴DE⊥平面PAE.∴平面PAE⊥平面PDE.∴过F作FG⊥PE于G,则 FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离.
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,∴FG=
a.∴点C到平面PDE的距离为
a.(或用等体积法求
| 2 |
即PA⊥AB.同理PA⊥AE.∵AB∩AE=A,∴PA⊥平面ABCDE.
(2)∵∠AED=90°,∴AE⊥ED.∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE,所以DE⊥AG.
∵PA=AE,G为PE中点,所以AG⊥PE,∴AG⊥平面PDE
(3)∵∠AED=90°,∴AE⊥ED.∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE.过A作AG⊥PE于G,过DE⊥AG,
∴AG⊥平面PDE.过G作GH⊥PD于H,连AH,由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角.
在直角△PAE中,AG=
| 2 |
2
| ||
| 3 |
| AG |
| AH |
3
| ||
| 10 |
∴二面角A-PD-E的正弦值为
3
| ||
| 10 |
(4)∵∠EAB=∠ABC=∠DEA=90°,BC=DE=a,AB=AE=2a,取AE中点F,连CF,∵AF∥=BC,∴四边形ABCF为平行四边形.∴CF∥AB,而AB∥DE,∴CF∥DE,而DE?平面PDE,CF?平面PDE,∴CF∥平面PDE.∴点C到平面PDE的距离等于F到平面PDE的距离.∵PA⊥平面ABCDE,∴PA⊥DE.又∵DE⊥AE,∴DE⊥平面PAE.∴平面PAE⊥平面PDE.∴过F作FG⊥PE于G,则 FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离.
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,∴FG=
| ||
| 2 |
| ||
| 2 |

点评:本题主要考查了在几何体中,线面垂直的证明,二面角,以及点到平面的距离求法,考查了学生的空间想象力,识图能力,逻辑推理能力,以及计算能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 四棱锥P-ABCD的三视图如图所示,四棱锥P-ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为
四棱锥P-ABCD的三视图如图所示,四棱锥P-ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为 (2013•虹口区一模)在正四棱锥P-ABCD中,侧棱PA的长为
(2013•虹口区一模)在正四棱锥P-ABCD中,侧棱PA的长为
