题目内容
在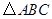 中,已知内角
中,已知内角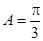 ,边
,边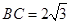 .设内角
.设内角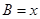 ,周长为
,周长为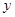 .
.
(1)求函数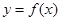 的解析式和定义域; (2)求
的解析式和定义域; (2)求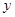 的最大值.
的最大值.
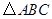 中,已知内角
中,已知内角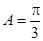 ,边
,边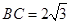 .设内角
.设内角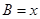 ,周长为
,周长为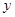 .
.(1)求函数
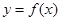 的解析式和定义域; (2)求
的解析式和定义域; (2)求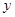 的最大值.
的最大值.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)已知两角一边,利用正弦定理将另外两条边用
 表示出来,即可表示
表示出来,即可表示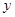 ,由
,由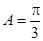 及内角和
及内角和 ,得
,得 ;(2)将
;(2)将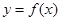 的解析式化为
的解析式化为 的形式,先由
的形式,先由 ,得
,得 的范围,再结合
的范围,再结合 的图象确定
的图象确定 的范围,进而求
的范围,进而求 的最大值.
的最大值.试题解析:(1)
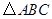 的内角和
的内角和 ,由
,由 得
得 ,由正弦定理知
,由正弦定理知 ,
, ,∵
,∵ ,∴
,∴ ; 6分
; 6分(2)因为

 ,∴
,∴ ,所以
,所以 ,所以,当
,所以,当 ,即
,即 时,
时,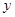 取得最大值
取得最大值 . -----------12分
. -----------12分 型函数的最大值.
型函数的最大值.
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
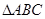 中,
中,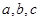 分别为角
分别为角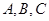 所对的边,向量
所对的边,向量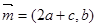 ,
, 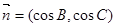 ,且
,且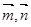 垂直.
垂直.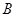 的大小;
的大小;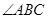 的平分线
的平分线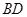 交
交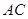 于点
于点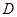 ,且
,且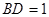 ,设
,设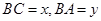 ,试确定
,试确定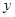 关于
关于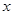 的函数式,并求边
的函数式,并求边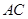 长的取值范围.
长的取值范围.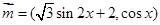 ,
,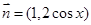 ,设函数
,设函数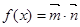 ,
,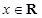 .
.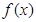 的最小正周期与最大值;
的最小正周期与最大值;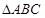 中,
中,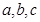 分别是角
分别是角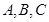 的对边,若
的对边,若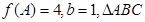 的面积为
的面积为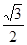 ,求
,求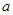 的值.
的值.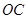 ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段 是以
是以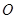 为顶点,
为顶点, 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段 是函数
是函数 ,
, 时的图象,图象的最高点为
时的图象,图象的最高点为 ,
, ,垂足为
,垂足为 .
.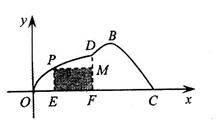
 的解析式;
的解析式; ,问:点
,问:点 落在曲线
落在曲线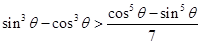 ,且
,且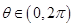 ,那么角
,那么角 的取值范围是_______.
的取值范围是_______.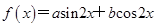 ,其中
,其中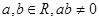 . 若
. 若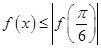 对一切
对一切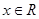 恒成立,则 ①
恒成立,则 ①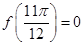 ; ②
; ② ; ③
; ③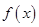 既不是奇函数也不是偶函数;④
既不是奇函数也不是偶函数;④ ;⑤ 存在经过点
;⑤ 存在经过点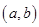 的直线与函数
的直线与函数 的始边与
的始边与 轴的非负半轴重合,终边过点
轴的非负半轴重合,终边过点 ,则
,则



 满足:
满足: ,
, ,则
,则



 ,则
,则 ( )
( )


