题目内容

已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图（其中横轴n表示日期，纵轴x表示气温），记A、B两城市这6天的最低气温平均数分别为 $数学公式$ 和 $数学公式$ ，标准差分别为s_A和s_B．则

A.
$数学公式$ ，s_A＞s_B
B.
$数学公式$ ，s_A＜s_B
C.
$数学公式$ ，s_A＞s_B
D.
$数学公式$ ，s_A＜s_B

C
分析：本题可以由折线图上的数据做出两个城市的平均气温和方差，也可以根据两个折线图的高低和变化的趋势即波动的大小，得到结果．
解答：由折线图可知A市的平均气温是 $\text{[math]}$ =6.25
B市的平均气温是 $\text{[math]}$ =11.7
由折线图也可以看出B市的气温较高，
可以看出B市的气温的变化不大方差较小，
故选C．
点评：求两组数据的平均值和方差是研究数据常做的两件事，平均值反映数据的平均水平，而方差反映数据的波动大小，从两个方面可以准确的把握数据的情况．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

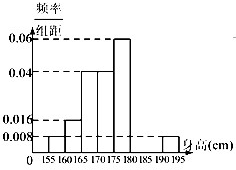从某校高三年级800名男生中随机抽取50名学生测量其身高，据测量被测学生的身高全部在155cm到195cm之间．将测量结果按如下方式分成8组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组得到的频率分布直方图的一部分．已知：第1组与第8组的人数相同，第6组、第7组和第8组的人数依次成等差数列．?
（1）求下列频率分布表中所标字母的值，并补充完成频率分布直方图；

分组	频数	频率	频率/组距
…	…	…	…
[180，185）	x	y	z
[185，190）	m	n	p
…	…	…	…

（2）若从身高属于第6组和第8组的所有男生中随机的抽取2名男生，记他们的身高分别为x、y，求满足：|x-y|≤5事件的概率．

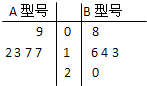某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：
（1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率P_A、P_B；
（2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
表一

等级利润产品	一等品	二等品
A型	4（万元）	3（万元）
B型	3（万元）	2（万元）

项目用量产品	配件（件）	资金（万元）
A型	6	4
B型	2	8

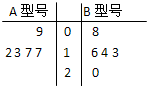某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：
（1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率P_A、P_B；
（2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
　　等级
利润
产品一等品二等品
A型 4（万元） 3（万元）
B型 3（万元） 2（万元）
表二
　　　　　　　
表二
　　项目
用量
产品配件（件）资金（万元）
A型 6 4
B型 2 8

某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品. 为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数. 现随机抽取了5组的质检记录，其一等品数如下面的茎叶图所示：

（1）试根据茎叶图所提供的数据，分别计算A、B两种

产品为一等品的概率PA、PB；

（2）已知每件产品的利润如表一所示，用、分别

表示一件A、B型产品的利润，在（1）的条件下，

求、的分布列及数学期望（均值）、；

（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设、分别表示生产A、B两种产品的数量，在（2）的条件下，求、为何值时，最大？最大值是多少？（解答时须给出图示）

某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60]分组，其频率分布直方图如右图所示，工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试，已知各年龄段两项培训结业考试成绩优秀的人数如下表所示，假设两项培训是相互独立的，结业考试也互不影响．

年龄分组	A项培训成绩优秀人数	B项培训成绩优秀人数
[20，30）	30	18
[30，40）	36	24
[40，50）	12	9
[50，60]	4	3

（1）若用分层抽样法从全厂工人中抽取一个容量为40的样本，求各年龄段应分别抽取的人数，并估计全厂工人的平均年龄；
（2）随机从年龄段[20，30）和[30，40）中各抽取1人，设这两人中A、B两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．