题目内容
某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品. 为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数. 现随机抽取了5组的质检记录，其一等品数如下面的茎叶图所示：
（1）试根据茎叶图所提供的数据，分别计算A、B两种
产品为一等品的概率PA、PB；
（2）已知每件产品的利润如表一所示，用
、
分别
表示一件A、B型产品的利润，在（1）的条件下，
求、
的分布列及数学期望（均值）
、
；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设
、
分别表示生产A、B两种产品的数量，在（2）的条件下，求、为何值时，
最大？最大值是多少？（解答时须给出图示）
 |
解：(1) 由茎叶图知 
；……………………………2分
. ……………………………4分
（2）随机变量、的分布列是
|
| 4 | 3 |
| P | 0.68 | 0.32 |
|
| 3 | 2 |
| P | 0.71 | 0.29 |
……………6分
∴ 
，
. ………8分
（3）由题设知
，目标函数为
，
………………………10分
作出可行域如图所示…………………12分
作直线l：
，
将向l右上方平移至l1位置时，即直线经过可行域上的点M时，
取最大值.
解方程组
，得
，
，
即，时，
取最大值，最大值是22.85. …………………………14分
练习册系列答案
相关题目
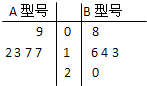某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：（1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率PA、PB；
（2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
表一
| 等级 利润 产品 |
一等品 | 二等品 |
| A型 | 4（万元） | 3（万元） |
| B型 | 3（万元） | 2（万元） |
| 项目 用量 产品 |
配件（件） | 资金（万元） |
| A型 | 6 | 4 |
| B型 | 2 | 8 |