题目内容
（本题共12分）如图所示，四边形ABCD是矩形，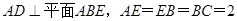
，F为CE上的点，且BF
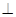平面ACE，AC与BD交于点G
（1）AE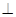平面BCE
（2）AE//平面BFD
（3）锥C-BGF的体积
【答案】
（1）略
（2）略
（3）三棱锥C-BGF的体积为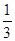
【解析】解：（1）∵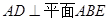 
又知四边形ABCD是矩形，故AD//BC
∴ 
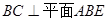故可知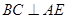 
………….1分
∵ BF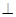
平面ACE ∴ BF 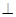AE
…………………………………………2分
又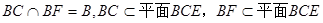 
∴ AE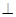平面BCE ………………………………………………………………4分
（2） 依题意，易知G为AC的中点
又∵ BF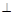
平面ACE 所以可知 BF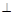EC，
又BE＝EC
∴ 可知F为CE的中点 ……………………………………………………………5分
故可知 GF//AE ……………………………………………………………………6分
又可知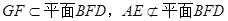 
∴ AE//平面BFD……………………………………………………………………..8分
(3) 由（1）可知AE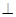平面BCE，又AE//GF
∴ GF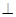平面BCE……………………………………………………………………9分
又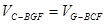 
所以GF的长为三棱锥G－BCF的高 GF＝
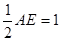. ....10分
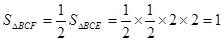………………………………………………11分
∴ 
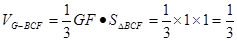
∴ 三棱锥C-BGF的体积为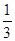……………………………………………………..12分
练习册系列答案
阅读快车系列答案
相关题目
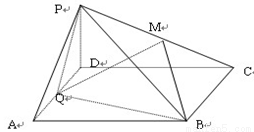
（本题满分共12分）如图，在
中，
为
边上高，
，
，沿
翻折，使得
，得到几何体
。（1）求证：
；
与平面
成角的正切值。
于D，PD与AO的延长线相交于点E，连接CE并延长交圆O于点F，连接AF。
时，求圆O的半径.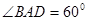
,Q为AD的中点
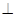平面PAD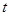
PC,试确定实数