题目内容
已知定义在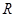 上的偶函数满足:
上的偶函数满足: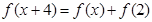 ,且当
,且当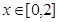 时,
时,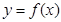 单调递减,给出以下四个命题:①
单调递减,给出以下四个命题:①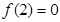 ;②
;②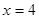 是函数
是函数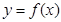 图像的一条对称轴;③函数
图像的一条对称轴;③函数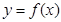 在区间
在区间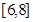 上单调递增;④若方程
上单调递增;④若方程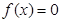 .在区间
.在区间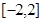 上有两根为
上有两根为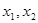 ,则
,则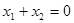 。以上命题正确的是 。(填序号)
。以上命题正确的是 。(填序号)
①②③④.
解析试题分析:∵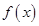 是定义在
是定义在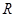 上的偶函数,∴
上的偶函数,∴ ,可得
,可得 ,在
,在 ,中令
,中令 得
得 ,∴函数
,∴函数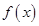 是周期为4的周期函数,又当
是周期为4的周期函数,又当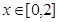 时,
时,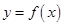 单调递减,结合函数的奇偶性画出函数
单调递减,结合函数的奇偶性画出函数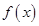 的简图,如图所示.从图中可以得出:②
的简图,如图所示.从图中可以得出:②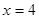 为函数
为函数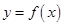 图象的一条对称轴;③函数
图象的一条对称轴;③函数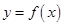 在
在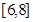 单调递增;④若方程
单调递增;④若方程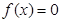 在
在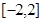 上的两根为
上的两根为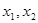 ,则
,则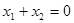 .故①②③④均正确.
.故①②③④均正确.
考点:
1.函数的单调性、奇偶性、对称性及周期性;2.函数的零点与方程的根.

练习册系列答案
相关题目
 对任意xÎ[2,4]恒成立,则m的取值范围为 .
对任意xÎ[2,4]恒成立,则m的取值范围为 . ,则
,则 .
. ,在
,在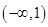 上单调递减,则a的取值范围是 .
上单调递减,则a的取值范围是 . 满足
满足 ,则
,则 的最大值为 .
的最大值为 .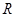 上的奇函数
上的奇函数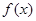 ,当
,当 时,
时,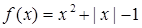 ,那么
,那么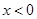 时,
时,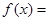 。
。 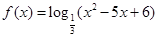 的单调递增区间为 .
的单调递增区间为 . 的值域是 .
的值域是 . 的图像和函数
的图像和函数 的图像的交点个数是 .
的图像的交点个数是 .