题目内容
已知函数f(x)=xlnx(x∈(0,+∞)
(I )求g(x)= 的单调区间与极大值;
的单调区间与极大值;
(II )任取两个不等的正数x1,x2,且x1<x2,若存在x0>0使f′(x0)= 成立,求证:x1<x0<x2
成立,求证:x1<x0<x2
(III)己知数列{an}满足a1=1,an+1=(1+ )an+
)an+ (n∈N+),求证:an<
(n∈N+),求证:an< (e为自然对数的底数).
(e为自然对数的底数).
(Ⅰ)解:由f(x)=xlnx(x∈(0,+∞)).
∴f(x+1)=(x+1)ln(x+1)(x∈(-1,+∞)).
则有 =
= =ln(x+1)-x,
=ln(x+1)-x,
此函数的定义域为(-1,+∞).
 .
.
故当x∈(-1,0)时,g′(x)>0;当x∈(0,+∞)时,g′(x)<0.
所以g(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞),
故g(x)的极大值是g(0)=0;
(Ⅱ)证明:由f(x)=xlnx(x∈(0,+∞)),得f′(x)=lnx+1,
所以 ,
,
于是 =
=
= ,
,
令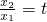 (t>1),则
(t>1),则 ,
,
因为t-1>0,只需证明lnt-t+1<0.
令s(t)=lnt-t+1,则 ,
,
∴s(t)在t∈(1,+∞)上递减,所以s(t)<s(1)=0,
于是h(t)<0,即lnx0<lnx2,故x0<x2.
同理可证x1<x0,故x1<x0<x2.
(Ⅲ)证明:因为a1=1, ,所以{an}单调递增,an≥1.
,所以{an}单调递增,an≥1.
于是 =
= ,
,
所以 (*).
(*).
由(Ⅰ)知当x>0时,ln(1+x)<x.
所以(*)式变为 .
.
即 (k∈N,k≥2),
(k∈N,k≥2),
令k=2,3,…,n,这n-1个式子相加得



=
=
= .
.
即 ,
,
所以 .
.
分析:(Ⅰ)由f(x)求出f(x+1),代入g(x),对函数g(x)求导后利用导函数的符号求出函数g(x)在定义域内的单调区间,从而求出函数的极大值;
(Ⅱ)求出f′(x0),代入f′(x0)= 后把lnx0用lnx1,lnx2表示,再把lnx0与lnx2作差后构造辅助函数,求导后得到构造的辅助函数的最大值小于0,从而得到lnx0<lnx2,运用同样的办法得到lnx1<lnx0,最后得到要证的结论;
后把lnx0用lnx1,lnx2表示,再把lnx0与lnx2作差后构造辅助函数,求导后得到构造的辅助函数的最大值小于0,从而得到lnx0<lnx2,运用同样的办法得到lnx1<lnx0,最后得到要证的结论;
(Ⅲ)由给出的递推式an+1=(1+ )an+
)an+ 说明数列{an}是递增数列,根据a1=1,得到an≥1,由此把递推式an+1=(1+
说明数列{an}是递增数列,根据a1=1,得到an≥1,由此把递推式an+1=(1+ )an+
)an+ 放大得到
放大得到 ,结合(Ⅰ)中的ln(1+x)<x得到
,结合(Ⅰ)中的ln(1+x)<x得到 ,分别取n=1,2,3,…,n-1,得到n个式子后累加即可证得结论.
,分别取n=1,2,3,…,n-1,得到n个式子后累加即可证得结论.
点评:本题考查了利用导数研究函数的单调性,考查了通过构造函数,利用函数的单调性和极值证明不等式,训练了累加法求数列的通项公式,考查了利用放缩法证明不等式,是一道难度较大的综合题型.
∴f(x+1)=(x+1)ln(x+1)(x∈(-1,+∞)).
则有
 =
= =ln(x+1)-x,
=ln(x+1)-x,此函数的定义域为(-1,+∞).
 .
.故当x∈(-1,0)时,g′(x)>0;当x∈(0,+∞)时,g′(x)<0.
所以g(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞),
故g(x)的极大值是g(0)=0;
(Ⅱ)证明:由f(x)=xlnx(x∈(0,+∞)),得f′(x)=lnx+1,
所以
 ,
,于是
 =
=
=
 ,
,令
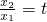 (t>1),则
(t>1),则 ,
,因为t-1>0,只需证明lnt-t+1<0.
令s(t)=lnt-t+1,则
 ,
,∴s(t)在t∈(1,+∞)上递减,所以s(t)<s(1)=0,
于是h(t)<0,即lnx0<lnx2,故x0<x2.
同理可证x1<x0,故x1<x0<x2.
(Ⅲ)证明:因为a1=1,
 ,所以{an}单调递增,an≥1.
,所以{an}单调递增,an≥1.于是
 =
= ,
,所以
 (*).
(*).由(Ⅰ)知当x>0时,ln(1+x)<x.
所以(*)式变为
 .
.即
 (k∈N,k≥2),
(k∈N,k≥2),令k=2,3,…,n,这n-1个式子相加得



=

=

=
 .
.即
 ,
,所以
 .
.分析:(Ⅰ)由f(x)求出f(x+1),代入g(x),对函数g(x)求导后利用导函数的符号求出函数g(x)在定义域内的单调区间,从而求出函数的极大值;
(Ⅱ)求出f′(x0),代入f′(x0)=
 后把lnx0用lnx1,lnx2表示,再把lnx0与lnx2作差后构造辅助函数,求导后得到构造的辅助函数的最大值小于0,从而得到lnx0<lnx2,运用同样的办法得到lnx1<lnx0,最后得到要证的结论;
后把lnx0用lnx1,lnx2表示,再把lnx0与lnx2作差后构造辅助函数,求导后得到构造的辅助函数的最大值小于0,从而得到lnx0<lnx2,运用同样的办法得到lnx1<lnx0,最后得到要证的结论;(Ⅲ)由给出的递推式an+1=(1+
 )an+
)an+ 说明数列{an}是递增数列,根据a1=1,得到an≥1,由此把递推式an+1=(1+
说明数列{an}是递增数列,根据a1=1,得到an≥1,由此把递推式an+1=(1+ )an+
)an+ 放大得到
放大得到 ,结合(Ⅰ)中的ln(1+x)<x得到
,结合(Ⅰ)中的ln(1+x)<x得到 ,分别取n=1,2,3,…,n-1,得到n个式子后累加即可证得结论.
,分别取n=1,2,3,…,n-1,得到n个式子后累加即可证得结论.点评:本题考查了利用导数研究函数的单调性,考查了通过构造函数,利用函数的单调性和极值证明不等式,训练了累加法求数列的通项公式,考查了利用放缩法证明不等式,是一道难度较大的综合题型.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|