Question

点O是△ABC所在平面上一点，若

OA

+

OB

+2

OC

=

0

，则△AOC的面积与△ABC的面积之比为（　　）

• A、

  1

  3

• B、

  2

  3

• C、

  1

  4

• D、

  1

  2

Answer 1

分析：根据题意，以OA、OB为一组邻边作?OADB，连接OD与AB交于点E，易得AB的中点为E，由平行四边形法则易得

OA

+

OB

=2

OE

将已知的向量等式变形，可得

OE

=-

OC

，分析可得O的AB边的中线OE上，且O为OE的中点；依次分析△AOC的面积与△ADC的面积之比以及△ADC的面积与△ABC的面积之比，即可得答案．

解答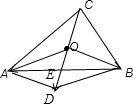：解：根据题意，以OA、OB为一组邻边作?OADB，连接OD与AB交于点E，
由平行四边形的性质易得AB的中点为E，
由平行四边形法则易得

OA

+

OB

=2

OE

又由

OA

+

OB

+2

OC

=

0

，可得

OA

+

OB

=-2

OC

，
则

OE

=-

OC

，
则O的AB边的中线OE上，且O为OE的中点，
O为OE的中点，△AOC的面积与△AEC的面积之比为1：2，
E为AB的中点，△AEC的面积与△ABC的面积之比为1：2，
则△AOC的面积与△ABC的面积之比为1：4，
故选C．

点评：本题考查向量的运算法则：关键是分析出O为AE的中点．