题目内容
几何体EFG —ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=l,AE= 。
。

(I)求证:EF⊥平面GDB;
(Ⅱ)线段DG上是否存在点M使直线BM与平面BEF所成的角为45°,若存在求等¥ 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(I)证明如下(Ⅱ)存在
【解析】
试题分析:证明:(1)由已知有 面
面 ,
,
 面
面 ,
,
连结 ,在正方形
,在正方形 中,
中, ,
, 面
面 ,
,
 面
面 ,
,
 且
且 ,
,
 为平行四边行,
为平行四边行, ,
,
 ,
, 面
面
解:(2)分别以 为
为 轴,
轴, 轴,
轴, 轴建立空间直角坐标系,
轴建立空间直角坐标系,
令 ,
,
 ,
,
令 为平面
为平面 的一个法向量,
的一个法向量, ,
,
令 ,
,
 ,
, ,
,
 ,
, 或
或 ,
,
 存在
存在 此时
此时
考点:直线与平面垂直的判定定理
点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。当然,此类题目也经常要我们求出几何体的体积和表面积。

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
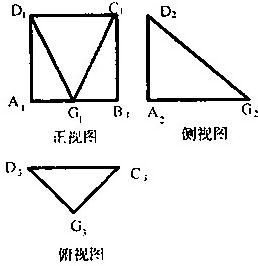 一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D,G在直立、侧立、水平三个投影面内的投影.在视图中,四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=
一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D,G在直立、侧立、水平三个投影面内的投影.在视图中,四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=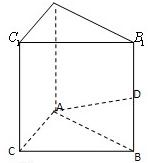 P是平面ABCD外的点,四边形ABCD是平行四边形,
P是平面ABCD外的点,四边形ABCD是平行四边形,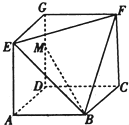 已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在DG上,若直线MB与平面BEF所角为45°,则DM=
已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在DG上,若直线MB与平面BEF所角为45°,则DM=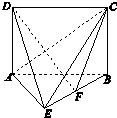 已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且AD=
已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且AD=