题目内容
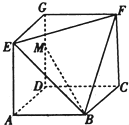 已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在DG上,若直线MB与平面BEF所角为45°,则DM=
已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在DG上,若直线MB与平面BEF所角为45°,则DM=分析:建立空间直角坐标系,求出平面BEF的法向量,根据直线MB与平面BEF所角为45°,利用向量的夹角公式,即可得出结论.
解答: 解:建立如图所示的空间直角坐标系,设DM=t,平面BEF的法向量为
解:建立如图所示的空间直角坐标系,设DM=t,平面BEF的法向量为
=(x,y,z),则∵
=(0,-1,1),
=(-1,0,1),
∴
,
令z=1,则x=y=1,∴
=(1,1,1),
∴cos<
,
>=
=
,
∵直线MB与平面BEF所角为45°,
∴|
|=
,
∴t=3
-4.
故答案为:3
-4.
 解:建立如图所示的空间直角坐标系,设DM=t,平面BEF的法向量为
解:建立如图所示的空间直角坐标系,设DM=t,平面BEF的法向量为| n |
| BE |
| BF |
∴
|
令z=1,则x=y=1,∴
| n |
∴cos<
| n |
| MB |
| ||||
|
|
| 2-t | ||||
|
∵直线MB与平面BEF所角为45°,
∴|
| 2-t | ||||
|
| ||
| 2 |
∴t=3
| 2 |
故答案为:3
| 2 |
点评:本题考查线面角,考查空间向量知识的运用,考查学生的计算能力,正确求出平面的法向量是关键.

练习册系列答案
相关题目
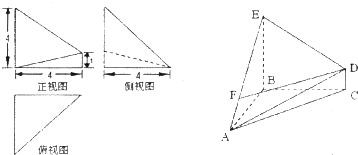
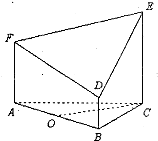 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点. 已知直角三角形ABC,其中∠ABC=60.,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60.,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.