题目内容
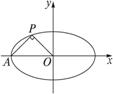
设椭圆
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(O为原点),求椭圆离心率的取值范围.
椭圆离心率的范围是(
,1).
解析:
如图,设P(x,y),由∠OPA=
知点P在以AO为直径的圆上,
即
.
联立方程组
消去y,得
(a2-b2)x2+a3x+a2b2=0.
解之,得x=-a或
.
当x=-a时,P与A重合,不满足题意,舍去.
故P点的横坐标为.
又∵
,∴a2>2b2,即a2>2(a2-c2).
∴
,
.
又∵0<e<1,
∴
1,即椭圆离心率的范围是(,1).
练习册系列答案
相关题目
，y
)、B(x
(a > b > 0) 上的两点，
，
= (
，
)，且满足
·
= 0，椭圆的离心率e = 
，短轴长为2，O为坐标原点．(1)求椭圆的方程；(2)若存在斜率为k的直线AB过椭圆的焦点F(0，c)(c为半焦距)，求直线AB的斜率k的值．
(a>b>0)的上、下两个顶点为A、B，直线l：
，点P是椭圆上异于点A、B的任意一点，连接AP并延长交直线l于点N，连接PB并延长交直线l于点M，设AP所在的直线的斜率为
，BP所在的直线的斜率为
．若椭圆的离心率为
，且过点
．
的值；
(a>b>0)的一个焦点，PQ是经过另一个焦点F2的弦，则△PF1Q的周长是（ ）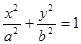
(a>b>0)
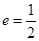，一条准线方程为x＝4 时，求椭圆方程；
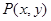是椭圆上一点，在（1）的条件下，求
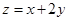的最大值及相应的P点坐标。