题目内容
15.在四边形ABCD中,AB∥CD,$\overrightarrow{AB}$$•\overrightarrow{BC}$=0,AB=2BC=2CD=2,则$\overrightarrow{AD}$在$\overrightarrow{CA}$上的投影为-$\frac{3\sqrt{5}}{5}$.分析 先建立坐标系,根据坐标的运算和向量的投影即可求出.
解答 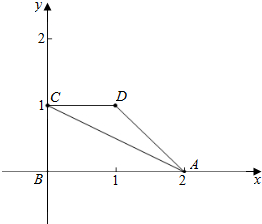 解:∵AB∥CD,$\overrightarrow{AB}$$•\overrightarrow{BC}$=0,AB=2BC=2CD=2,
解:∵AB∥CD,$\overrightarrow{AB}$$•\overrightarrow{BC}$=0,AB=2BC=2CD=2,
以B为坐标原点,以BA为x轴,BC为y轴,建立如图所示的坐标系,
∴A(2,0),C(0,1),D(1,1),
∴$\overrightarrow{AD}$=(-1,1),$\overrightarrow{AC}$=(-2,1),
∴$\overrightarrow{AD}$•$\overrightarrow{AC}$=-1×(-2)+1×1=3,|$\overrightarrow{AC}$|=$\sqrt{5}$,
∴$\overrightarrow{AD}$在$\overrightarrow{CA}$上的投影为$\frac{\overrightarrow{AD}•\overrightarrow{AC}}{|\overrightarrow{AC}|}$=-$\frac{3}{\sqrt{5}}$=-$\frac{3\sqrt{5}}{5}$,
故答案为:-$\frac{3\sqrt{5}}{5}$.
点评 本题考查了向量的坐标运算以及向量的投影,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{\frac{3x-1}{x+3}(x≠-3)}\\{a(x=-3)}\end{array}\right.$的定义域与值域相同,则常数α=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
 如图,已知椭圆C的一个顶点(0,-1),焦点在x轴上,若右焦点到直线x-y+2$\sqrt{2}$=0的距离为3.
如图,已知椭圆C的一个顶点(0,-1),焦点在x轴上,若右焦点到直线x-y+2$\sqrt{2}$=0的距离为3.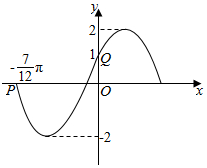 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.