题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)试判断函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析; (Ⅱ) ![]()
【解析】
(Ⅰ)求出原函数的导函数,然后对a分类,当a≤0时,![]() <0,f(x)为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各段内的符号得到原函数的单调性;
<0,f(x)为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各段内的符号得到原函数的单调性;
(Ⅱ)分离参数t,可得![]() 恒成立.令
恒成立.令![]() ,则问题等价于求解函数g(x)的最小值,然后利用导数分析求解函数g(x)的最小值得答案.
,则问题等价于求解函数g(x)的最小值,然后利用导数分析求解函数g(x)的最小值得答案.
(Ⅰ)由题可得函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)当![]() 时,
时,![]() ,
,
则不等式![]() 可化为
可化为![]() ,
,
因为不等式![]() 恒成立,所以原问题可转化为
恒成立,所以原问题可转化为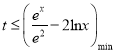 .
.
设![]() ,显然函数
,显然函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某公司的甲、乙两名工程师因为工作需要,各自选购一台笔记本电脑.该公司提供了![]() 三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
型号 |
|
|
|
销量(台) | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比,乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比,且他们两人选购笔记本电脑互不影响.
(1)求甲、乙两人选购不同款笔记本电脑的概率;
(2)若公司给购买这三款笔记本电脑的员工一定的补贴,补贴标准如下表:
型号 |
|
|
|
补贴(千元) | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为![]() 千元,求
千元,求![]() 的分布列和数学期望.
的分布列和数学期望.
