题目内容
已知函数f(x)=4x3-3x2cosθ+(1)当cosθ=0时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(3)若对(2)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
解:(1)当cosθ=0时,f(x)=4x3,则f(x)在(-∞,+∞)内是增函数,故无极值.
(2)f′(x)=12x2-6xcosθ,令f′(x)=0,得x1=0,x2=![]() .
.
由(1),只需分下面两种情况讨论:
①当cosθ>0时,随x的变化,f′(x)的符号及f(x)的变化情况如下表:
x | (-∞,0) | 0 | (0, |
| ( |
f′(x) | + | 0 | - | 0 | + |
f(x) | ?↗ | 极大值 | ↙? | 极小值 | ↗? |
因此,函数f(x)在x=![]() 处取得极小值f(
处取得极小值f(![]() ),
),
且f(![]() )=-
)=-![]() cos3θ+
cos3θ+![]() cosθ.
cosθ.
要使f(![]() )>0,必有-
)>0,必有-![]() cosθ(cos2θ-
cosθ(cos2θ-![]() )>0,
)>0,
可得0<cosθ<![]() ;
;
由于0≤θ≤2π,故![]() <θ<
<θ<![]() 或
或![]() <θ<
<θ<![]() .
.
②当cosθ<0时,随x的变化,f′(x)的符号及f(x)的变化情况如下表:
x | (-∞, |
| ( | 0 | (0,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ?↘ | 极小值 | ↗? |
因此函数f(x)在x=0处取得极小值f(0),且f(0)=![]() cosθ.
cosθ.
若f(0)>0,则cosθ>0,矛盾,所以当cosθ<0时,f(x)的极小值不会大于零.
综上,要使函数f(x)在(-∞,+∞)内的极小值大于零,参数θ的取值范围为(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() ).
).
(3)由(2)知,函数f(x)在区间(-∞,0)与(![]() ,+∞)内都是增函数,
,+∞)内都是增函数,
由题设,函数f(x)在(2a-1,a)内是增函数,则a需满足不等式组
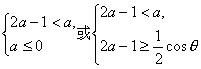
由(2),参数θ∈(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() )时,0<cosθ<
)时,0<cosθ<![]() ,要使不等式2a-1
,要使不等式2a-1![]()
![]() 关于参数θ恒成立,必有2a-1≥
关于参数θ恒成立,必有2a-1≥![]() ,即
,即![]() ≤a.
≤a.
综上,解得a≤0或![]() ≤a<1,
≤a<1,
所以a的取值范围是(-∞,0]∪[![]() ,1).
,1).

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |