题目内容
如图所示,在三棱柱ABC-A′B′C′中,四边形A′ABB′是菱形,四边形BCC′B′是矩形,C′B′⊥AB.
(1)求证:平面CA′B⊥平面A′AB;
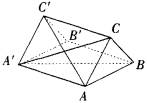
(2)若C′B′=3,AB=4,∠ABB′=60°,求AC′与平面BCC′B′所成角的大小(用反三角函数表示).
答案:
解析:
解析:
(1)证明:∵ 在三棱柱ABC-A′B′C′中,C′B′∥CB ∴ CB⊥AB,又∵ CB⊥BB′,AB∩BB′=B ∴ CB⊥平面A′AB.∵ CB ∴ 平面CA′B⊥平面A′AB. (2)解:由四边形A′ABB′是菱形,∠ABB′=60° 连结AB′可知△ABB′是正三角形 取BB′中点H,连结AH,则AH⊥BB′,如图所示 又由CB⊥平面A′AB,得平面A′ABB′⊥平面C′B′BC 而AH垂直于两平面交线BB′ ∴ AH⊥平面C′B′BC,连结C′H 则∠AC′H为AC′与平面BCC′B′所成的角 AB′=4,AH= AC′= 在Rt△AHC′中,sin∠AC′H= ∴ ∠AC′H= ∴ 直线AC′与平面BCC′B′所成的角是
|

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
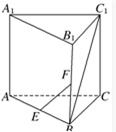 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |

 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心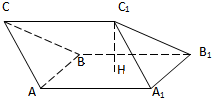 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心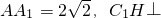 平面AA1B1B且
平面AA1B1B且 .
.
