题目内容
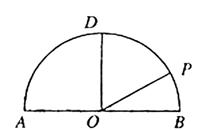
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.

(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.若△OEF的面积不小于2![]() ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.
(Ⅰ)解法1:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2), P(![]() ),依题意得
),依题意得
||MA|-|MB||=|PA|-|PB|
=![]() <|AB|=4.
<|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设实半轴长为a,虚半轴长为b,半焦距为c,
则c=2,2a=2![]() ,∴a2=2,b2=c2-a2=2.
,∴a2=2,b2=c2-a2=2.
∴曲线C的方程为![]() .
.
解法2:同解法1建立平面直角坐标系,则依题意可得||MA|-|MB||=|PA|-|PB|<|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设双曲线的方程为![]() >0,b>0).
>0,b>0).
则由  解得a2=b2=2,
解得a2=b2=2,
∴曲线C的方程为![]()

图1 图2
(Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理得
(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴ 
![]()

∴k∈(-![]() ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,![]() ).
).
设E(x1,y1),F(x2,y2),则由①式得x1+x2=![]() ,于是
,于是
|EF|=![]()
=
而原点O到直线l的距离d=![]() ,
,
∴S△DEF=
若△OEF面积不小于2![]() ,即S△OEF
,即S△OEF![]() ,则有
,则有
 ③
③
综合②、③知,直线l的斜率的取值范围为[-![]() ,-1)∪(1-,1) ∪(1,
,-1)∪(1-,1) ∪(1, ![]() ]
]
解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴ 
![]()

∴k∈(-![]() ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,![]() ).
).
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|= ③
③
当E、F在同一支上时(如图1所示),
S△OEF=![]()
当E、F在不同支上时(如图2所示).
![]() S△ODE=
S△ODE=![]()
综上得S△OEF=![]() 于是
于是
由|OD|=2及③式,得S△OEF=
若△OEF面积不小于2![]()
 ④
④
综合②、④知,直线l的斜率的取值范围为[-![]() ,-1]∪(-1,1)∪(1,
,-1]∪(-1,1)∪(1,![]() ).
).

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案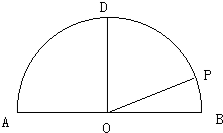 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.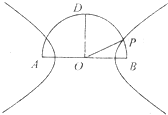 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.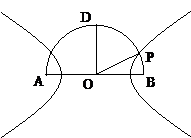
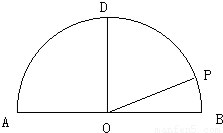 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.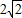 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.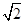 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。