题目内容
定义域为R,且对任意实数x1,x2都满足不等式f( )≤
)≤ 的所有函数f(x)组成的集合记为M,例如,函数f(x)=kx+b∈M.
的所有函数f(x)组成的集合记为M,例如,函数f(x)=kx+b∈M.(1)已知函数f(x)=
 ,证明:f(x)∈M;
,证明:f(x)∈M;(2)写出一个函数f(x),使得f(x)∉M,并说明理由;
(3)写出一个函数f(x)∈M,使得数列极限

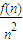 =1,
=1,
 =1.
=1.
【答案】分析:(1)分类讨论,验证f(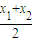 )≤
)≤ 成立,即可得到结论;
成立,即可得到结论;
(2)利用条件,构造函数f(x)=-x2,f(x)∉M,再取值验证即可;
(3)利用条件,构造函数f(x)=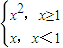 满足f(x)∈M,验证条件即可.
满足f(x)∈M,验证条件即可.
解答:解:(1)证明:由题意,当x1≤x2≤0或0≤x1≤x2时,f(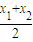 )≤
)≤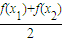 成立
成立
设x1≤0≤x2,且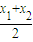 <0,
<0,
∵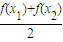 -f(
-f(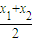 )=
)=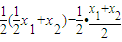 =
=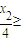
∴f(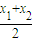 )≤
)≤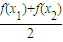 成立
成立
设x1≤0≤x2,且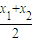 ≥0,
≥0,
∵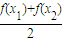 -f(
-f(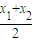 )=
)=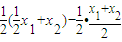 =
=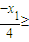
∴f(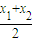 )≤
)≤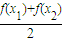 成立
成立
∴综上所述,f(x)∈M;
(2)如函数f(x)=-x2,f(x)∉M
取x1=-1,x2=1,则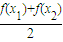 =-1,f(
=-1,f(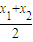 )=0
)=0
此时f(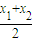 )≤
)≤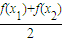 不成立;
不成立;
(3)f(x)=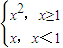 满足f(x)∈M,且
满足f(x)∈M,且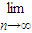
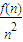 =
=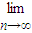
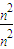 =1,
=1,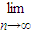
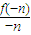 =
=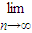
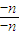 =1.
=1.
点评:本题考查新定义,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.
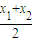 )≤
)≤ 成立,即可得到结论;
成立,即可得到结论;(2)利用条件,构造函数f(x)=-x2,f(x)∉M,再取值验证即可;
(3)利用条件,构造函数f(x)=
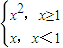 满足f(x)∈M,验证条件即可.
满足f(x)∈M,验证条件即可.解答:解:(1)证明:由题意,当x1≤x2≤0或0≤x1≤x2时,f(
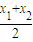 )≤
)≤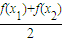 成立
成立设x1≤0≤x2,且
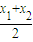 <0,
<0,∵
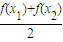 -f(
-f(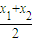 )=
)=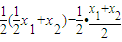 =
=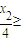
∴f(
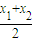 )≤
)≤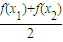 成立
成立设x1≤0≤x2,且
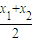 ≥0,
≥0,∵
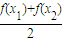 -f(
-f(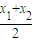 )=
)=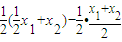 =
=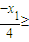
∴f(
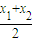 )≤
)≤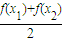 成立
成立∴综上所述,f(x)∈M;
(2)如函数f(x)=-x2,f(x)∉M
取x1=-1,x2=1,则
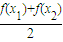 =-1,f(
=-1,f(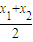 )=0
)=0此时f(
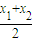 )≤
)≤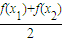 不成立;
不成立;(3)f(x)=
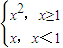 满足f(x)∈M,且
满足f(x)∈M,且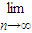
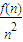 =
=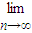
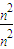 =1,
=1,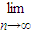
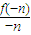 =
=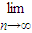
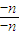 =1.
=1.点评:本题考查新定义,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目