题目内容
在某次考试中,要从20道题中随机地抽出6道题,若考生至少能答对其中的4道题即可通过;若至少能答对其中5道题就获得优秀,已知某考生能答对其中10道题,并且知道他在这次考试中已经通过,求他获得优秀成绩的概率.
思路分析: 本题属于条件概率问题.在已知该考生在考试中通过的前提下,获得优秀的概率,所以应根据条件概率的公式求解.
解:设事件A为“该考生6道题全答对”,事件B为“该考生答对了其中5道题另一道答错”,事件C为“该考生答对了其中4道题另2道答错”,事件D为“该考生在这次考试中通过”,事件E为“该考生在这次考试中获得优秀”,则A、B、C两两互斥,且D=A∪B∪C,E=A∪B.由古典概型的概率公式及加法公式可知
P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)=![]() ;
;
P(AD)=P(A),P(BD)=P(C∪B);
P(E|D)=P(A∪B|D)=P(A|D)+P(B|D)=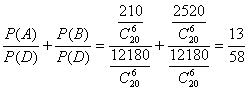 ,所以所求的概率为
,所以所求的概率为![]() .
.
误区警示 利用公式P(B∪C|A)=P(B|A)+P(C|A)可使求有些条件概率较为简捷,但应请注意这个性质在“B与C互斥”这一前提下才具备的,因此不要忽视这一条件而乱用这个公式.

练习册系列答案
相关题目
在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.
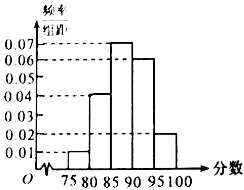
(1)下表是这次抽查成绩的频数分布表,试求正整数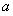 、
、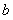 的值;
的值;
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 50 | a | 350 | 300 | b |
(2)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求抽取成绩为优秀的学生人数;
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
(1)请在如图的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
(2)要从4名语文成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的英语成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.

| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
(2)要从4名语文成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的英语成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.

 (2012•朝阳区一模)某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(2012•朝阳区一模)某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀. 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示: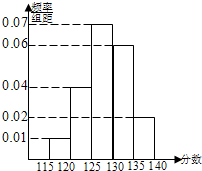 某校在一次“诊断性”考试中,对该年级的1000名考生的数学成绩进行统计分析,成绩的频率分布直方图如图所示,规定125及其以上为优秀.
某校在一次“诊断性”考试中,对该年级的1000名考生的数学成绩进行统计分析,成绩的频率分布直方图如图所示,规定125及其以上为优秀.