题目内容
20. 己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )
己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )| A. | 2 | B. | $\frac{{3+\sqrt{2}}}{2}$ | C. | 4 | D. | $\sqrt{2}+1$ |
分析 根据几何体的三视图,得出该几何体有2个面是直角边为1的等腰直角三角形,
有2个面为直角边长为1和$\sqrt{2}$的直角三角形,求出该几何体的表面积即可.
解答 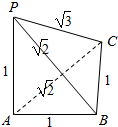 解:由几何体的三视图知,
解:由几何体的三视图知,
该几何体有两个面是直角边为1的等腰直角三角形,
有两个面为直角边长为1和$\sqrt{2}$的直角三角形,
如图所示;
所以,该三棱锥的表面积为
S=2×$\frac{1}{2}$×1×1+2×$\frac{1}{2}$×1×$\sqrt{2}$=$\sqrt{2}$+1.
故选:D.
点评 本题考查了空间几何体三视图的应用问题,解题时应根据三视图还原出几何体的结构特征,是基础题目.

练习册系列答案
相关题目
8.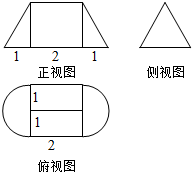 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D. | 2$\sqrt{3}$+$\sqrt{3}$π |
12.若a>1,b>1,log2a•log2b=16,则log2(ab)的最小值为( )
| A. | -4 | B. | 8 | C. | -8 | D. | 4 |
10.函数y=2sinx-1的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
