题目内容
已知以点A(-1,2)为圆心的圆与直线
：
相切.
过点B(-2,0)的动直线
与圆A相交与
、
两点，
是
的中点，直线
与相交于点
.
(I) 求圆A的方程；
（II）当
时，求直线的方程；
（III）
是否为定值，如果是，求出定值；如果不是，请说明理由.
同下
解析:
设圆A的半径为
,由于圆A与直线
：
相切，
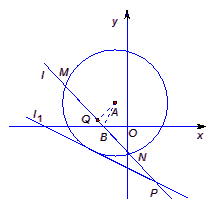
……………………………………………………….2分
圆A的方程为
……………………………………….4分
(II) ①当直线
与
轴垂直时, 易知
符合题意……………5分
②当直线与轴不垂直时,
设直线的方程为
，即
，
连结
,则
∵
，∴
，………………………………………6分
则由
，得
, ∴直线：
.
故直线的方程为或………………………………………9分
(III)∵
,∴ 
…10分
当与轴垂直时，易得
，则
,又
,
∴
………………………………………………………11分
②当的斜率存在时，设直线的方程为，
则由
，得
（
）,则
∴
综上所述，
是定值，且
.…………………14分
练习册系列答案
相关题目
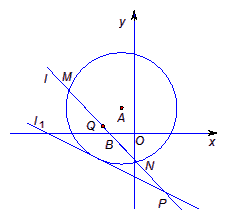
已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交与M、N两点，Q是MN的中点，直线l与l1相交于点P．
如图所示，已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P．
·
=0，且|
|=|
|+2.