题目内容
如图,直三棱柱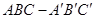 的侧棱长为3,
的侧棱长为3,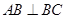 ,且
,且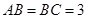 ,
,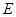 、
、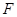 分别是棱
分别是棱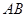 、
、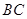 上的动点,且
上的动点,且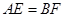
(1)证明:无论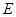 在何处,总有
在何处,总有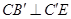 ;
;
(2)当三棱柱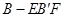 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线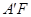 与
与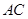 所成角的余弦值.
所成角的余弦值.

【答案】
(1)详见解析;(2) .
.
【解析】
试题分析:(1)利用正方形的性质,线面垂直的判定与性质定理求解;(2)利用三棱柱的体积公式,均值不等式求得.
试题解析:

(1)∵ 是正方形,∴
是正方形,∴ ,
,
又 ,
, ,
,
∴ 平面
平面 ,
(4分)
,
(4分)
∴ ,
, 平面
平面 ,
,
又 平面
平面 ,∴
,∴ .
(6分)
.
(6分)
(2)设三棱锥 的体积为
的体积为 ,
,
当 时取等号,
(8分)
时取等号,
(8分)
故当 时,即
时,即 、
、 分别是棱
分别是棱 、
、 上的中点时,体积最大,
上的中点时,体积最大,
则 为所求.
为所求.
∴ ,
, ,
, ,∴
,∴ . (12分)
. (12分)
考点:三棱柱的性质,体积,均值不等式,最值.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为( )


| A、4 | ||
B、
| ||
C、2
| ||
| D、2 |
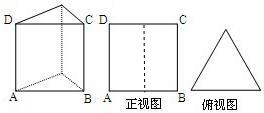 如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为
如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其左视图的面积为
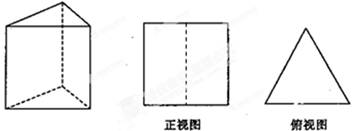
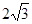 B.
B.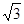 C.4
D.2
C.4
D.2