题目内容
已知梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,
![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ∥
∥![]() ,
,![]() ,
,![]() 是
是![]() 的中点.沿
的中点.沿![]() 将梯形
将梯形![]() 翻折,使平面
翻折,使平面![]() ⊥平面
⊥平面![]() (如图) .
(如图) .


(Ⅰ) 当![]() 时,求证:
时,求证:![]() ⊥
⊥![]() ;
;
(Ⅱ) 若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)当![]() 取得最大值时,求二面角
取得最大值时,求二面角![]() 的余弦值.
的余弦值.
解:(Ⅰ)(法一)作![]() 于
于![]() ,连
,连![]() ,
,![]()

由平面![]() 平面
平面![]() 知
知 ![]() 平面
平面![]()
而![]() 平面
平面![]() ,故
,故![]() 又四边形
又四边形![]() 为正方形
为正方形
∴ ![]()
又![]() ,故
,故![]() 平面
平面![]() 而
而![]() 平面
平面![]()
∴ ![]() . (或者直接利用三垂线定理得出结果)
. (或者直接利用三垂线定理得出结果)
(法二)∵ 平面![]() 平面
平面![]()
![]()
∴ ![]() ⊥面平面
⊥面平面![]()
∴ ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,又
,又![]() ⊥
⊥![]()
故可如图建立空间坐标系![]() .
.

则![]()
![]() ,
,![]() ,
,![]()
∴ ![]()
∴ ![]() .
.
(Ⅱ) ∵ ![]() ,面
,面![]() 面
面![]()
∴ ![]() 面
面![]()
又由(Ⅰ)![]() 平面
平面![]() ∴
∴ ![]()
所以 ![]()
![]() =
=![]()
![]()
![]()
![]()
即![]() 时
时![]() 有最大值为
有最大值为![]() .
.
(Ⅲ)(法一)作![]() 于
于![]() ,作
,作![]() ,连
,连![]()

由三垂线定理知![]()
∴ ![]() 是二面角
是二面角![]() 的平面角的补角
的平面角的补角
由![]() ∽
∽![]() ,知
,知 ![]()
而![]() ,
,![]()
![]()
∴ ![]() 又
又![]()
∴ 在![]() 中,
中,![]()
因为∠是![]() 锐角 ∴
锐角 ∴![]() ∠
∠![]() =
=![]()
而∠![]() 是二面角
是二面角![]() 的平面角的补角
的平面角的补角
故二面角![]() 的余弦值为-
的余弦值为-![]() .
.
(法二)设平面![]() 的法向量为
的法向量为![]()
∵ ![]() ,
,![]() ,
,![]() ,
,![]()
∴ ![]()
![]()
则 即
即![]()
取 ![]() 则
则 ![]() ∴
∴ ![]()
面![]() 的一个法向量为
的一个法向量为![]()
则![]() <
<![]() >
>
由于所求二面角![]() 的平面角为钝角,
的平面角为钝角,
所以,此二面角的余弦值为-![]() .
.

练习册系列答案
相关题目


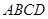 中
中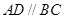 ,
,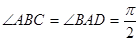 ,
,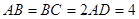 ,
,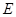 、
、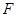 分别是
分别是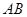 、
、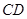 上的点,
上的点,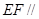
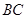 ,
,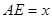 .沿
.沿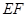 将梯形
将梯形 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图).
(如图). 是
是
 时,求证:
时,求证: ⊥
⊥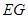 ;
;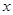 变化时,求三棱锥
变化时,求三棱锥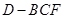 体积的最大值.
体积的最大值. 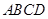 中,
中, ∥
∥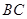 ,
,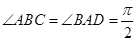 ,
,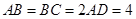 ,
, 、
、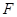 分别是
分别是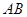 、
、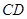 上的点,
上的点, ∥
∥ ,
, 是
是 ⊥平面
⊥平面 (如图).
(如图).

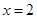 时,求证:
时,求证: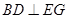 ;
;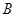 、
、 、
、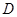 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的余弦值.
的余弦值.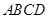 中,
中,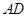 ∥
∥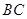 ,
,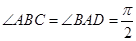 ,
,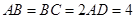 ,
,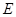 、
、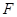 分别是
分别是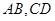 上的点,
上的点,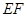 ∥
∥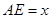 ,
,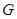 是
是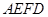 ⊥平面
⊥平面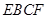 (如图) .
(如图) .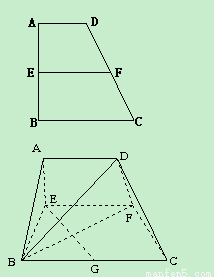
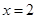 时,求证:
时,求证: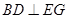 ;
; 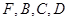 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为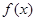 ,求
,求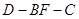 的余弦值.
的余弦值. 中,
中, ,
, 。求梯形的高.
。求梯形的高.