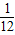Question

设-1≤a≤1，0≤b≤1，则关于x的方程x²+2ax+b=0有实根的概率是（　　）

• A．

  1

  3

• B．

  2

  3

• C．

  1

  6

• D．

  1

  12

Answer 1

分析：这是一个几何概型问题，关于x的方程x²+2ax+b=0有实根根据判别式大于等于零，可以得到a和b之间的关系，写出对应的集合，做出面积，得到概率．

解答：解：方程x²+2ax+b=0有实根?△≥0?4a²-4b≥0?b≤a²，
（1）点（a，b）所构成的区域为Ω={（a，b）|-1≤a≤1，0≤b≤1}，
面积S_Ω=2×1=2；
设“方程有实根”为事件A，所对应的区域为A={（a，b）|-1≤a≤1，0≤b≤1，b≤a²}，
其面积S_A=

∫

1 -1

a²da=

1

3

a³

|

1 -1

=

2

3

，
这是一个几何概型，所以P（A）=

SA

SΩ

=

1

3

．
故选A．

点评：古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，概率的值是通过长度、面积、和体积的比值得到．