Question

解答须写出文字说明、证明过程和演算步骤．

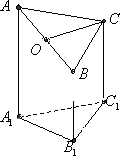
下图是一个直三棱柱(以A₁B₁C₁为底面)，被一平面所截得的几何体，截面为ABC．已知A₁B₁＝B₁C₁＝1，∠A₁B₁C₁＝90°，AA₁＝4，BB₁＝2，CC₁＝3

(Ⅰ)设点O是AB的中点，证明：OC∥平面A₁B₁C₁

(Ⅱ)求AB与平面AA₁CC₁所成角的正弦值．

Answer 1

答案：
解析：

解：(Ⅰ)证明：作OD∥AA1交A1B1于D，连C1D． 　　则OD∥BB1∥CC1， 　　因为O是AB的中点， 　　所以． 　　则ODC1C是平行四边形，因此有∥C1D， 　　C1D平面C1B1A1，且OC平面C1B1A1 　　则OC∥面A1B1C1． 　　(Ⅱ)解：如图，过B作截面BA2C2∥面A1B1C1，分别交AA1，CC1于A2，C2， 　　作BH⊥A2C2于H， 　　因为平面A2BC2⊥平面AA1C1C，则BH⊥面AA1C1C． 　　连结AH，则∠BAH就是AB与面AA1C1C所成的角． 　　因为BH＝，AB＝，所以． 　　所以AB与面AA1C1C所成的角的正弦值为． 　　解法二： 　　(Ⅰ)证明：如图，以B1为原点建立空间直角坐标系，则A(0，1，4)，B(0，0，2)，C(1，0，3)，因为O是AB的中点，所以，， 　　易知，是平面A1B1C1的一个法向量． 　　由且平面A1B1C1知OC∥平面A1B1C1． 　　(Ⅱ)设AB与面AA1C1C所成的角为θ． 　　求得，． 　　设是平面AA1C1C的一个法向量，则由得， 　　取x＝y＝1得：． 　　又因为 　　所以，，则． 　　所以AB与面AA1C1C所成的角的正弦值为．