题目内容
若函数 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
A
解析试题分析:解:当a<0时,-a>0,若af(-a)>0,即f(-a)=log2(-a)<0,解得0<-a<1∴-1<a<0当a>0时,-a<0,若af(-a)>0,即f(-a)= >0,解得0<a<1,综上实数a的取值范围是(-1,0)∪(0,1),故选A .
>0,解得0<a<1,综上实数a的取值范围是(-1,0)∪(0,1),故选A .
考点:奇偶性与单调性的综合.

练习册系列答案
相关题目
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使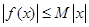 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:②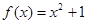 :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 对任意的
对任意的 满足
满足 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A. | B. | C. | D. |
(2013•浙江)已知a、b、c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
| A.a>0,4a+b=0 | B.a<0,4a+b=0 |
| C.a>0,2a+b=0 | D.a<0,2a+b=0 |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.[1,+∞) |
| C.(0,1] | D.(0,1) |
已知函数 ,则不等式x+(x+1)f(x+1)≤1的解集是( )
,则不等式x+(x+1)f(x+1)≤1的解集是( )
A. | B.{x|x≤1} |
C. | D. |
已知定义在R上的奇函数f(x),满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数,则( )
| A.f(﹣25)<f(11)<f(80) |
| B.f(80)<f(11)<f(﹣25) |
| C.f(11)<f(80)<f(﹣25) |
| D.f(﹣25)<f(80)<f(11) |
 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )


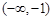

 ﹣1的图象大致是( )
﹣1的图象大致是( )


