题目内容
已知椭圆C: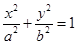 的离心率等于
的离心率等于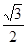 ,点P
,点P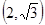 在椭圆上。
在椭圆上。
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左右顶点分别为
的左右顶点分别为 ,过点
,过点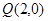 的动直线
的动直线 与椭圆
与椭圆 相交于
相交于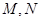 两点,是否存在定直线
两点,是否存在定直线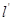 :
: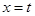 ,使得
,使得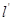 与
与 的交点
的交点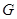 总在直线
总在直线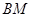 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的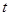 值;若不存在,说明理由.
值;若不存在,说明理由.
(1) ;(2)存在,
;(2)存在, .
.
解析试题分析:(1)由 ,点
,点 代入椭圆方程,二者联立可以解出
代入椭圆方程,二者联立可以解出 ;(2)以
;(2)以 的存在性分两种情况:①
的存在性分两种情况:① 不存在,直线
不存在,直线 :
: ,易证符合题意;②
,易证符合题意;② 存在时,设直线
存在时,设直线 :
: ,用直线方程和椭圆方程联立方程组,消参得一元二次方程,利用韦达定理得,
,用直线方程和椭圆方程联立方程组,消参得一元二次方程,利用韦达定理得, ,又因为
,又因为 共线,有
共线,有 ,由
,由 得
得 ,得出
,得出 ,由于
,由于 成立,所以点
成立,所以点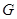 在直线
在直线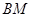 上,综上:存在定直线
上,综上:存在定直线 :
: ,使得
,使得 与
与 的交点
的交点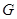 总在直线
总在直线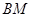 上,
上,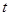 的值是
的值是 .
.
试题解析:(1)由 , 2分
, 2分
又点 在椭圆上,
在椭圆上, , 4分
, 4分
所以椭圆方程是: ; 5分
; 5分
(2)当 垂直
垂直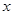 轴时,
轴时, ,则
,则 的方程是:
的方程是: ,
,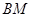 的方程是:
的方程是: ,交点
,交点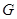 的坐标是:
的坐标是: ,猜测:存在常数
,猜测:存在常数 ,
,
即直线 的方程是:
的方程是: 使得
使得 与
与 的交点
的交点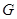 总在直线
总在直线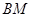 上, 6分
上, 6分
证明:设 的方程是
的方程是 ,点
,点 ,
,
将 的方程代入椭圆
的方程代入椭圆 的方程得到:
的方程得到: ,
,
即: , 7分
, 7分
从而: , 8分
, 8分
因为: ,
,
 共线
共线
所以: ,
, , 9分
, 9分
又 ,
,
要证明 共线,即要证明
共线,即要证明 , 10分
, 10分
即证明: ,
,
即: ,
,
即:

练习册系列答案
相关题目
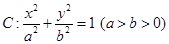 的右焦点为
的右焦点为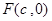 ,上顶点为B,离心率为
,上顶点为B,离心率为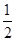 ,圆
,圆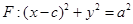 与
与 轴交于
轴交于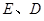 两点
两点 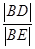 的值;
的值;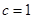 ,过点
,过点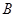 与圆
与圆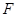 相切的直线
相切的直线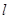 与
与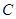 的另一交点为
的另一交点为 ,求
,求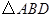 的面积
的面积 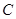 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为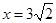 ,离心率为
,离心率为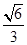 .若直线
.若直线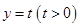 与椭圆
与椭圆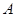 、
、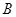 ,以线段
,以线段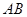 为直径作圆
为直径作圆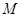 .
.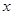 轴相切,求圆
轴相切,求圆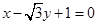 截得的线段长.
截得的线段长.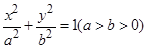 的长轴两端点分别为
的长轴两端点分别为 ,
,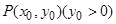 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使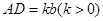 ,
,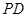 交
交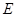 ,
, 交
交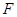 .
.
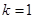 ,且
,且 为椭圆上顶点时,
为椭圆上顶点时,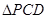 的面积为12,点
的面积为12,点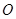 到直线
到直线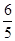 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: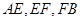 成等比数列.
成等比数列.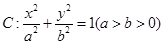 的离心率为
的离心率为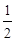 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线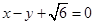 相切,直线
相切,直线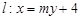 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.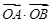 的取值范围;
的取值范围;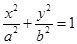 的离心率等于
的离心率等于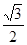 ,点P
,点P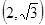 在椭圆上。
在椭圆上。 的方程;
的方程;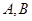 ,过点
,过点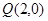 的动直线
的动直线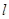 与椭圆
与椭圆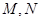 两点,是否存在定直线
两点,是否存在定直线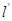 :
: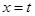 ,使得
,使得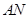 的交点
的交点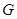 总在直线
总在直线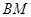 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的 值;若不存在,说明理由.
值;若不存在,说明理由.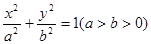 的离心率为
的离心率为 ,
, :y=x+2与原点为圆心,以椭圆C的短轴长为直
:y=x+2与原点为圆心,以椭圆C的短轴长为直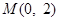 的直线
的直线 与椭圆
与椭圆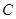 交于
交于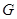 ,
,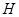 两点.设直线
两点.设直线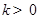 ,在
,在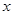 轴上是否存在点
轴上是否存在点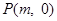 ,使得
,使得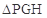 是以GH为底边的等腰三角形. 如果存在,求出实数
是以GH为底边的等腰三角形. 如果存在,求出实数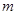 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.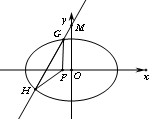
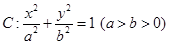 的右焦点为
的右焦点为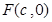 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆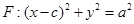 与
与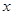 轴交于
轴交于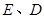 两点
两点 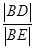 的值;
的值;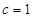 ,过点
,过点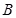 与圆
与圆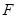 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求 的面积
的面积 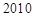 年
年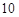 月
月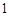 日
日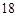 时
时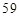 分
分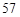 秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约
秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约 公里、远地点高度约
公里、远地点高度约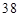 万公里的直接奔月椭圆(地球球心
万公里的直接奔月椭圆(地球球心 为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面
为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面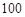 公里、近月面
公里、近月面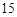 公里(月球球心
公里(月球球心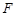 为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以
为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以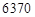 公里,月球半径约为
公里,月球半径约为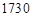 公里。
公里。