题目内容
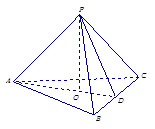
(12分)如图,已知三棱锥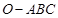 的侧棱
的侧棱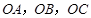 两两垂直,且
两两垂直,且 ,
,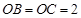 ,
,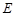 是
是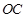 的中点.
的中点.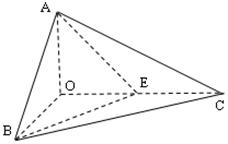
(Ⅰ)求异面直线 与
与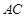 所成角的余弦值;
所成角的余弦值;
(Ⅱ)BE和平面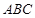 所成角的正弦值.
所成角的正弦值.
(1) .(2)
.(2)
解析试题分析:(I)利用空间向量法求异面直线所成的角,先建系,然后再利用 来解决.
来解决.
(II)先求出平面ABC的法向量,然后再利用设EF与平面ABC的所成的角为 ,再利用
,再利用 求解即可.
求解即可.
(1)以 为原点,
为原点, 、
、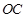 、
、 分别为
分别为 、
、 、
、 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则有 、
、 、
、 、
、

 <
< >
> 所以异面直线
所以异面直线 与
与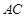 所成角的余弦为
所成角的余弦为 .
.
(2)设平面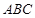 的法向量为
的法向量为 则
则
由
由
 ,
,
则 ,故BE和平面
,故BE和平面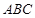 的所成的角正弦值为
的所成的角正弦值为
考点:空间的角,空间向量法求角.
点评:掌握空间的各种角的定义以及用向量法求解的方法及步骤是解决此类问题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 的侧面
的侧面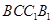 是菱形,
是菱形,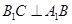 .
.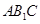
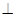 平面
平面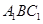 ;
;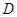 是
是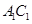 上的点,且
上的点,且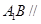 平面
平面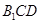 ,求
,求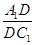 的值.
的值.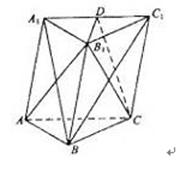
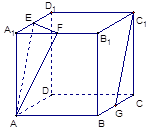
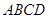 和矩形
和矩形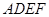 所在平面相互垂直,
所在平面相互垂直,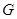 是
是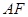 的中点.
的中点. 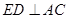 ;
;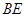 与平面
与平面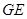 与
与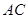 所成角的余弦值.
所成角的余弦值.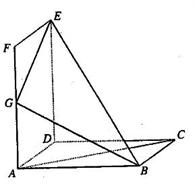
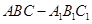 的侧棱与底面垂直,
的侧棱与底面垂直,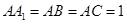 ,
,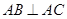 ,
, ,
,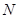 分别是
分别是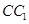 ,
,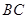 的中点,点
的中点,点 在直线
在直线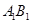 上,且
上,且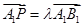 ;
;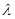 取何值,总有
取何值,总有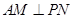 ;
;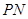 与平面
与平面 所成的角
所成的角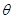 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;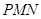 与平面
与平面
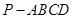 中,底面
中,底面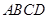 为平行四边形,
为平行四边形,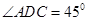 ,
,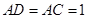 ,
, 为
为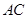 中点,
中点,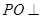 平面
平面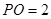 ,
,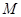 为
为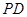 中点.
中点. //平面
//平面 ;
; 平面
平面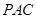 ;
;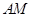 与平面
与平面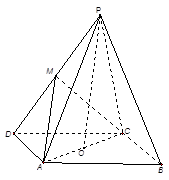
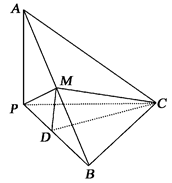
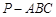 中,
中,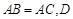 为
为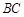 的中点,
的中点,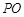 平面
平面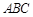 ,垂足
,垂足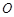 落在线段
落在线段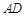 上,已知
上,已知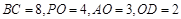
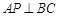 ;
;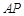 上是否存在点
上是否存在点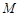 ,使得二面角
,使得二面角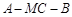 为直二面角?若存在,求出
为直二面角?若存在,求出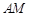 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.