题目内容
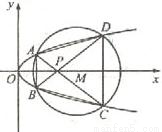
如图,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.
【答案】分析:(1)先联立抛物线与圆的方程消去y,得到x的二次方程,根据抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.
(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.
解答:解:(Ⅰ)将抛物线E:y2=x代入圆M:(x-4)2+y2=r2(r>0)的方程,
消去y2,整理得x2-7x+16-r2=0(1)
抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:
方程(1)有两个不相等的正根
∴
即 .
.
解这个方程组得 ,
, .
.
(II)设四个交点的坐标分别为
 、
、 、
、 、
、 .
.
则由(I)根据韦达定理有x1+x2=7,x1x2=16-r2,
则
∴
令 ,
,
则S2=(7+2t)2(7-2t)下面求S2的最大值.
由三次均值有:

当且仅当7+2t=14-4t,即 时取最大值.
时取最大值.
经检验此时 满足题意.
满足题意.
故所求的点P的坐标为 .
.
点评:本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.
(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.
解答:解:(Ⅰ)将抛物线E:y2=x代入圆M:(x-4)2+y2=r2(r>0)的方程,
消去y2,整理得x2-7x+16-r2=0(1)
抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:
方程(1)有两个不相等的正根
∴

即
 .
.解这个方程组得
 ,
, .
.(II)设四个交点的坐标分别为
 、
、 、
、 、
、 .
.则由(I)根据韦达定理有x1+x2=7,x1x2=16-r2,

则

∴

令
 ,
,则S2=(7+2t)2(7-2t)下面求S2的最大值.
由三次均值有:


当且仅当7+2t=14-4t,即
 时取最大值.
时取最大值.经检验此时
 满足题意.
满足题意.故所求的点P的坐标为
 .
.点评:本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
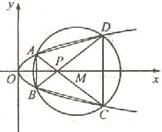 如图,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.
如图,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.

