Question

如图,ABCD是边长为1的正方形,M、N分别是DA、BC上的点,且MN∥AB,现沿MN折成直二面角AB-MN-CD.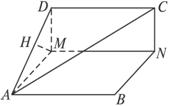

(1)求证:平面ADC⊥平面AMD;

(2)设AM=x(0＜x＜1),MN到平面ADC的距离为y,试用x表示y;

(3)点M在什么位置时,y有最大值,最大值为多少?

Answer 1

(1)证明:∵ABCD是正方形,且MN∥AB∥CD,

    ∴MN⊥AM,MN⊥DM,即CD⊥AM,CD⊥DM.

    ∴CD⊥平面AMD.

    ∵CD平面ADC,∴平面ADC⊥平面AMD.

(2)解:∵MN∥CD,

    ∴MN∥平面ADC.故MN到平面ADC的距离即为M到平面ADC的距离.

    过M作MH⊥AD于H,

    ∵平面ADC⊥平面AMD,

    ∴MH⊥平面ADC,即MH为所求距离.

    在Rt△AMD中,求得y==(0＜x＜1).

(3)解:y≤=≤,当且仅当x=1-x,即x=时,y_max=,此时M为AD的中点.