题目内容
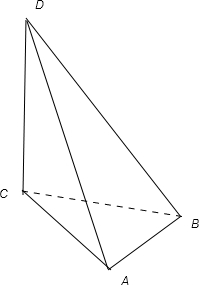
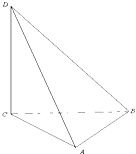 如图,直三棱锥D-ABC,已知DC⊥平面ABC,AB=20米,从点A处看到点D的仰角为60°,∠ABC=30°,∠BAC=105°,分别求AD、BD的长(精确到0.01米)
如图,直三棱锥D-ABC,已知DC⊥平面ABC,AB=20米,从点A处看到点D的仰角为60°,∠ABC=30°,∠BAC=105°,分别求AD、BD的长(精确到0.01米)
分析:在△ABC中,∠ACB=45°结合正弦定理
=
可求AC;在Rt△DCA中,∠ACD=60°及所求AC,可求CD,AD;在△ABC中,由正弦定理
=
可求BC;最后由勾股定理可得,BD=
,可求BD
| AB |
| sin∠ACB |
| AC |
| sin∠BAC |
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
| BC2+CD2 |
解答:解:在△ABC中,∠ACB=45°由正弦定理可得:
=
解得AC=10
在Rt△DCA中,∠DAC=60°则CD=10
,AD=20
≈28.28
在△ABC中,由正弦定理可得:
=
解得,BC=10+10
由勾股定理可得,BD=
=10
≈36.69
综上可得,AD≈28.28米,BD≈36.69米
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
解得AC=10
| 2 |
在Rt△DCA中,∠DAC=60°则CD=10
| 6 |
| 2 |
在△ABC中,由正弦定理可得:
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
解得,BC=10+10
| 3 |
由勾股定理可得,BD=
| BC2+CD2 |
10+2
|
综上可得,AD≈28.28米,BD≈36.69米

点评:结合已知条件反复利用解三角形的常用工具:正弦定理,勾股定理是解决本题的关键,解三角形的两大常用工具:正弦定理、余弦定理,在解决问题时对公式的选择,主要结合题目中已知条件的特点:边及对角一般利用正弦定理;边及夹角,一般利用余弦定理.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
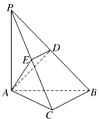 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.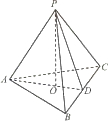 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,