题目内容
在△ABC中,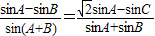 .
.(I)求B;
(Ⅱ)若
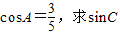 的值.
的值.
【答案】分析:(I)整理题设中的等式可知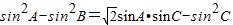 ,利用正弦定理把角的正弦转化成边,进而代入到余弦定理中即可求得cosB的值,进而求得B.
,利用正弦定理把角的正弦转化成边,进而代入到余弦定理中即可求得cosB的值,进而求得B.
(II)根据cosA,利用同角三角函数基本关系求得sinA,进而根据.sinC=sin(A+B)利用正弦的两角和公式求得答案.
解答:解:(I)∵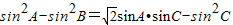 ,
,
由正弦定理得: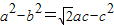 ,∴
,∴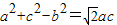 ,
,
由余弦定理得: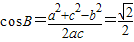 ,又B∈(0,π)∴
,又B∈(0,π)∴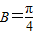
(II)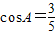 ,所以
,所以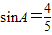 ,
,
所以sinC=sin(A+B)=sinAcosB+cosAsinB=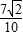 .
.
点评:本题主要考查了正弦定理和余弦定理,及两角和公式的运用.考查了考生综合分析问题和基本的运用的能力.
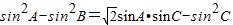 ,利用正弦定理把角的正弦转化成边,进而代入到余弦定理中即可求得cosB的值,进而求得B.
,利用正弦定理把角的正弦转化成边,进而代入到余弦定理中即可求得cosB的值,进而求得B.(II)根据cosA,利用同角三角函数基本关系求得sinA,进而根据.sinC=sin(A+B)利用正弦的两角和公式求得答案.
解答:解:(I)∵
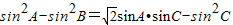 ,
,由正弦定理得:
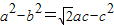 ,∴
,∴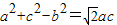 ,
,由余弦定理得:
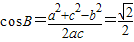 ,又B∈(0,π)∴
,又B∈(0,π)∴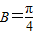
(II)
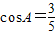 ,所以
,所以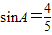 ,
,所以sinC=sin(A+B)=sinAcosB+cosAsinB=
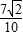 .
.点评:本题主要考查了正弦定理和余弦定理,及两角和公式的运用.考查了考生综合分析问题和基本的运用的能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 ABC中,
ABC中, , sinB=
, sinB= .
. ,求
,求 ABC中,
ABC中, ,
sinB=
,
sinB= .
. ,求
,求