题目内容
若非零函数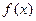 对任意实数
对任意实数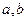 均有
均有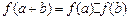 ,
,
且当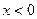 时,
时,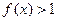 .
.
(1)求证: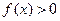 ;
;
(2)求证: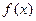 为减函数;
为减函数;
(3)当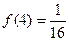 时,解不等式
时,解不等式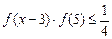
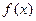 对任意实数
对任意实数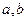 均有
均有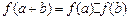 ,
,且当
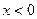 时,
时,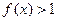 .
. (1)求证:
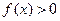 ;
; (2)求证:
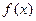 为减函数;
为减函数;(3)当
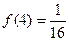 时,解不等式
时,解不等式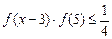
解:(1)
(2)设 则
则

 ,
,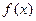 为减函数
为减函数
(3)由
原不等式转化为 ,结合(2)得:
,结合(2)得:
故不等式的解集为

(2)设
 则
则

 ,
,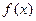 为减函数
为减函数(3)由

原不等式转化为
 ,结合(2)得:
,结合(2)得:
故不等式的解集为

同答案

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
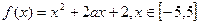 .
.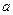 的范围,使
的范围,使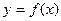 在区间
在区间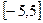 上是单调函数。 (2)求
上是单调函数。 (2)求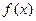 的最小值
的最小值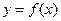 是奇函数,对于任意
是奇函数,对于任意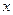 、
、 R都有
R都有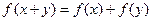 ,且当
,且当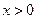 时,
时,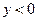 ,
,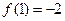 ,求函数
,求函数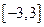 上的最大值和最小值.
上的最大值和最小值.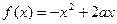 与
与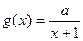 在区间
在区间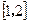 上都是减函数,则a的取值范围是( )
上都是减函数,则a的取值范围是( )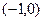
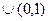 B
B 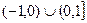 C
C 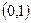 D
D 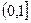
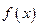 满足
满足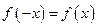 ,如果函数
,如果函数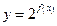 在
在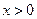 时是增函数,则在
时是增函数,则在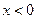 时,是增函数还是减函数?试证明.
时,是增函数还是减函数?试证明.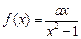 (
(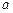 ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。 ,都有
,都有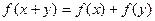 ,且
,且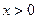 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.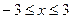 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.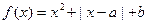 在区间
在区间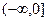 上为减函数,则实数
上为减函数,则实数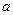 的取值范围是( )
的取值范围是( )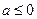 ;
;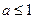 ;
;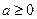 ;
;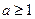
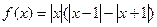 是( )
是( )