题目内容
已知函数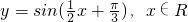 .
.
(1)求函数y的最大值及y取最大值时x的集合; (2)求函数y的单调递减区间;
(3)将函数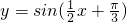 的图象作怎样的变换可得到y=sinx的图象?
的图象作怎样的变换可得到y=sinx的图象?
解:(1)当 时,y取最大值ymax=1,…(1分)
时,y取最大值ymax=1,…(1分)
此时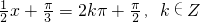 即
即 …(3分)∴y取最大值1时,x的集合为
…(3分)∴y取最大值1时,x的集合为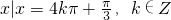 …(4分)
…(4分)
(2)令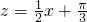 ,则y=sinz,y=sinz的单调递减区间为
,则y=sinz,y=sinz的单调递减区间为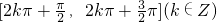
由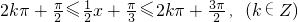 得
得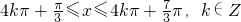
又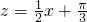 在(-∞,+∞)上为增函数,故原函数的单调递减区间为:
在(-∞,+∞)上为增函数,故原函数的单调递减区间为: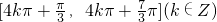 …(8分)
…(8分)
(3)将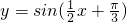 的图象向右平移
的图象向右平移 个单位可得到
个单位可得到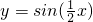 的图象,…(10分)
的图象,…(10分)
再将所得图象的横坐标变为原来的 可得到y=sinx的图象.…(12分)
可得到y=sinx的图象.…(12分)
分析:(1)根据正弦函数的特点知当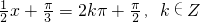 时y取最大值为1,求出x即可得出结果.
时y取最大值为1,求出x即可得出结果.
(2)直接根据正弦函数的单调性进行求单调区间.
(3)将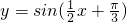 的图象向右平移
的图象向右平移 个单位可得到
个单位可得到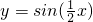 的图象,再将所得图象的横坐标变为原来的
的图象,再将所得图象的横坐标变为原来的 可得到y=sinx的图象.
可得到y=sinx的图象.
点评:本题考查了正弦函数的值域,单调性以及函数的图象变换,对于三角函数的基本性质一定要熟练掌握,这是解题的关键.
 时,y取最大值ymax=1,…(1分)
时,y取最大值ymax=1,…(1分)此时
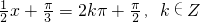 即
即 …(3分)∴y取最大值1时,x的集合为
…(3分)∴y取最大值1时,x的集合为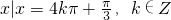 …(4分)
…(4分)(2)令
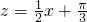 ,则y=sinz,y=sinz的单调递减区间为
,则y=sinz,y=sinz的单调递减区间为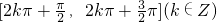
由
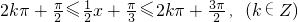 得
得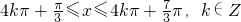
又
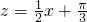 在(-∞,+∞)上为增函数,故原函数的单调递减区间为:
在(-∞,+∞)上为增函数,故原函数的单调递减区间为: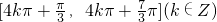 …(8分)
…(8分)(3)将
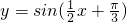 的图象向右平移
的图象向右平移 个单位可得到
个单位可得到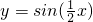 的图象,…(10分)
的图象,…(10分)再将所得图象的横坐标变为原来的
 可得到y=sinx的图象.…(12分)
可得到y=sinx的图象.…(12分)分析:(1)根据正弦函数的特点知当
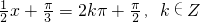 时y取最大值为1,求出x即可得出结果.
时y取最大值为1,求出x即可得出结果.(2)直接根据正弦函数的单调性进行求单调区间.
(3)将
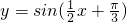 的图象向右平移
的图象向右平移 个单位可得到
个单位可得到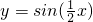 的图象,再将所得图象的横坐标变为原来的
的图象,再将所得图象的横坐标变为原来的 可得到y=sinx的图象.
可得到y=sinx的图象.点评:本题考查了正弦函数的值域,单调性以及函数的图象变换,对于三角函数的基本性质一定要熟练掌握,这是解题的关键.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.