Question

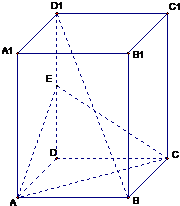如图，在正四棱柱ABCD-A₁B₁C₁D₁中，AC为底面ABCD的对角线，E为D₁D的中点
（Ⅰ）求证：D₁B⊥AC；
（Ⅱ）求证：D₁B∥平面AEC．

Answer 1

分析：（I）连接BD，由正四棱柱的结构特征，用正方形对角线互相垂直的性质，结合线面垂直的判定定理我们可以证明出AC⊥平面D₁DB，进而根据线面垂直的性质得到D₁B⊥AC；
（Ⅱ）BD∩AC=O，连接OE，由三角形中位线定理，我们可得D₁B∥EO，再由线面平行的判定定理，即可得到D₁B∥平面AEC．

解答：证明：（Ⅰ）连接BD
在正四棱柱ABCD-A₁B₁C₁D₁中DD₁⊥平面ABCD，ABCD是正方形

∵DD1⊥平面ABCD， AC?平面ABCD ∴DD1⊥AC ∵ABCD是正方形 ∴AC⊥BD

∵DD1⊥AC，AC⊥BD，BD∩DD1=D ∴AC⊥平面D1DB ∵D1B?平面D1DB ∴AC⊥D1B

（Ⅱ）设BD∩AC=O，连接OE

∵ABCD是正方形 ∴BO=DO ∵E是D1D的中点 ∴EO是△D1DB的中位线 ∴D1B∥EO ∵D1B?平面AEC，EO?平面AEC ∴D1B∥平面AEC

点评：本题考查的知识点是直线与平面垂直的性质及直线与平面平行的判定，其中熟练掌握空间线、面之间位置关系的判定、性质、定义是解答本题的关键．