题目内容
(满分14分)随机将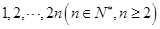 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为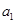 ,最大数为
,最大数为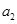 ;B组最小数为
;B组最小数为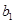 ,最大数为
,最大数为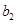 ,记
,记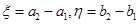
(1)当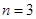 时,求
时,求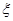 的分布列和数学期望;
的分布列和数学期望;
(2)令C表示事件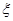 与
与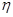 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率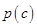 ;
;
(3)对(2)中的事件C,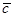 表示C的对立事件,判断
表示C的对立事件,判断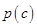 和
和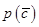 的大小关系,并说明理由。
的大小关系,并说明理由。
(1)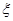
2 3 4 5 P 



 (2)当
(2)当 时,
时, ,当
,当 时
时
(3)当 时,
时, 当
当 时,
时,
解析试题分析:(1)当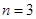 时,将6个正整数平均分成A,B两组,不同的分组方法共有
时,将6个正整数平均分成A,B两组,不同的分组方法共有 种,
种,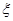 所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为
所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为 ,
, ,
, ,
, ,
, (2)
(2)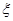 和
和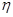 恰好相等的所有可能值为
恰好相等的所有可能值为 当
当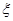 和
和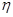 恰好相等且等于
恰好相等且等于 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当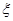 和
和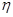 恰好相等且等于
恰好相等且等于 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当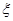 和
和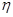 恰好相等且等于
恰好相等且等于 时,不同的分组方法有2
时,不同的分组方法有2 种;当
种;当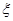 和
和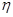 恰好相等且等于
恰好相等且等于 时,不同的分组方法有2
时,不同的分组方法有2 种;以此类推:
种;以此类推: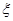 和
和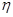 恰好相等且等于
恰好相等且等于 时,不同的分组方法有2
时,不同的分组方法有2 种;所以当
种;所以当 时,
时,
当 时
时 (3)先归纳:当
(3)先归纳:当 时,
时, 因此
因此 当
当 时,
时, 即证当
即证当 时
时
 ,这可用数学归纳法证明. 当
,这可用数学归纳法证明. 当 时,
时, ,利用阶乘作差
,利用阶乘作差 可得大小.
可得大小.
试题解析:(1)当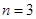 时,
时,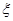 所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有
所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有 种,所以
种,所以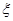 的分布列为
的分布列为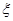
2 3 4 5 P 




(2)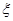 和
和
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: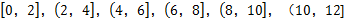 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.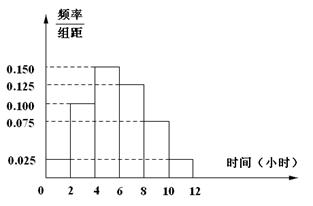
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有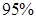 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附: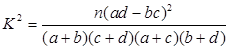
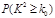 | 0.10 | 0.05 | 0.010 | 0.005 |
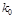 | 2.706 | 3.841 | 6.635 | 7.879 |
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“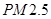 ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“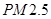 ” ” 小时平均浓度( 小时平均浓度(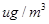 ) ) |  |  |  |  |  |  |  |  |  |  |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘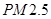 ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率. 某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(1)求当天商品不进货的概率;
(2)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取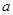 ,
,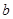 ,
,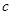 .
.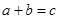 ”的概率;
”的概率; ,第二次出现的点数为
,第二次出现的点数为 .
.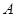 为“
为“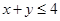 ”,求
”,求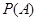 ;
;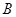 为“
为“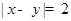 ”,求
”,求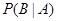 .
.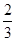 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的. 万元,若新产品
万元,若新产品 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.