Question

已知椭圆C：3x²+4y²=12，试确定m的取值范围，使得对于直线l：y=4x+m，椭圆上有不同的两点A、B关于这条直线对称.

Answer 1

分析：本题可用对称的实质即直线AB与l垂直，线段AB的中点在l上，联立直线AB与椭圆方程利用判别式求解；又因存在关于l对称的两点A、B，所以AB的中点在l上，由直线AB与直线l垂直，知k_AB=，故可用“点差法”求出AB中点M的坐标，然后利用点M在椭圆内部去求解.

解：设A（x₁,y₁）,B(x₂,y₂)，AB的中点M（x₀,y₀）.

则

两式相减得3(x₁+x₂)(x₁-x₂)+4(y₁+y₂)(y₁-y₂)=0,

即.

所以y₀=3x₀.又M（x₀,y₀）在直线l上，

所以

解得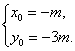

因为点M（-m,-3m）在椭圆内部，

所以3(-m)²+4(-3m)²＜12,

即.

所以m的取值范围为m∈(,).