题目内容
在数列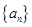 中,
中,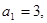
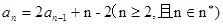
(1)求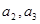 的值;
的值;
(2)证明:数列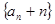 是等比数列,并求
是等比数列,并求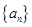 的通项公式;
的通项公式;
(3)求数列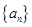 的前n项和
的前n项和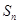 .
.
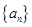 中,
中,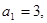
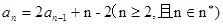
(1)求
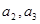 的值;
的值;(2)证明:数列
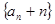 是等比数列,并求
是等比数列,并求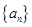 的通项公式;
的通项公式;(3)求数列
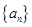 的前n项和
的前n项和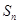 .
.(1) ;(2)证明详见解析,
;(2)证明详见解析, ;(3)
;(3) .
.
 ;(2)证明详见解析,
;(2)证明详见解析, ;(3)
;(3) .
.试题分析:(1)赋值:令
 ;(2)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,∴利用等比数列的定义证明,利用等比数列通项公式可求出
;(2)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,∴利用等比数列的定义证明,利用等比数列通项公式可求出
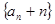 的通项公式,从而求出
的通项公式,从而求出 ;(3)根据通项公式求
;(3)根据通项公式求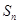 ,常用方法有裂项相消法,错位相减法,分组求和法,奇偶并项求和法.
,常用方法有裂项相消法,错位相减法,分组求和法,奇偶并项求和法.试题解析:(1)令
 ,
, 令
令 ,
, .
.(2)
 ,∴数列
,∴数列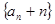 是首项为4,公比为2的等比数列,∴
是首项为4,公比为2的等比数列,∴ .
.(3)∵数列
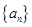 的通项公式
的通项公式 ,∴
,∴
 .
. 项和.
项和.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
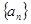 的前
的前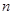 项和为
项和为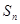 ,已知
,已知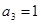 ,
,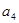 是
是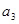 和
和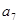 的等比中项.
的等比中项.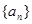 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中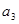 是
是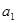 与
与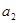 的等差中项.
的等差中项. 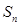
 中,
中, (
( ).
). 的值;
的值; ,使得数列
,使得数列 是一个等差数列?若存在,求
是一个等差数列?若存在,求 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.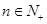 ,都有
,都有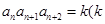 为常数
为常数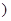 ,那么这个数列叫做等积数列,
,那么这个数列叫做等积数列,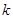 叫做这个数列的公积.已知数列
叫做这个数列的公积.已知数列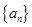 是等积数列,且
是等积数列,且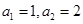 ,公积为
,公积为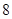 ,则
,则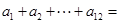 ( )
( )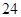
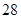
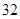
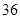
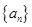 、
、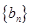 都是等差数列,若
都是等差数列,若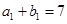 ,
,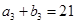 ,则
,则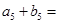 .
.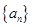
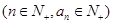 ,若
,若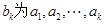 中最大值
中最大值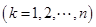 ,则称数列
,则称数列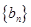 为数列
为数列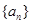 中,
中,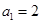 ,
, 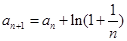 ,则
,则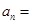 ( )
( )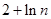
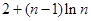
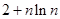
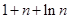
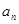 }的前n项和为
}的前n项和为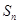 ,且
,且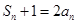 ,则使不等式
,则使不等式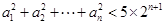 成立的n的最大值为 .
成立的n的最大值为 .