题目内容
设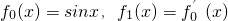
，
，
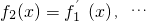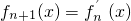，n∈N，则f2011（x）=________．
-cosx
分析：由（sinx）（4）=sinx，可得，∴fn+4（x）=fn（x），据此可求出答案．
解答：∵（sinx）′=cosx，（cosx）′=-sinx，（-sinx）′=-cosx，（-cosx）′=sinx，
∴fn+4（x）=fn（x），
∴f2011（x）=f3（x）=-cosx．
故答案是-cosx．
点评：本题考查了三角函数的导数，理解三角函数的导函数具有周期性是解决此问题的关键．
分析：由（sinx）（4）=sinx，可得，∴fn+4（x）=fn（x），据此可求出答案．
解答：∵（sinx）′=cosx，（cosx）′=-sinx，（-sinx）′=-cosx，（-cosx）′=sinx，
∴fn+4（x）=fn（x），
∴f2011（x）=f3（x）=-cosx．
故答案是-cosx．
点评：本题考查了三角函数的导数，理解三角函数的导函数具有周期性是解决此问题的关键．
练习册系列答案
相关题目
设函数f(x)=x2-x+
的定义域是[n，n+1]，n∈N*，则f（x）的值域中所含整数的个数是（ ）
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、2n个 |
（2012•怀化二模）如图，一个树形图依据下列规律不断生长：1个空心圆点到下一行仅生长出1个实心圆点，1个实心圆点到下一行生长出1个实心圆点和1个空心圆点．则第8行的实心圆点的个数是