题目内容
(2007•武汉模拟)(文)设数列{an}的前n项和Sn=
,n=1,2,3…(1)求数列{an}的通项公式an.(2)求数列{
}的前n项和Tn.
| n |
| n+1 |
| 1 |
| an |
分析:(1)由数列{an}的前n项和Sn=
可求a1,n≥2,an=Sn-Sn-1,验证n=1时是否满足,满足则合;
(2)由(1)求得an=
,
=n2+n,利用分组求和的方法可求
.
| n |
| n+1 |
(2)由(1)求得an=
| 1 |
| n(n+1) |
| 1 |
| an |
| n |
 |
| i=1 |
| 1 |
| ai |
解答:(文) 解:(1)∵数列{ an}的前n项和Sn=
知a1=S1=
又由an=Sn-Sn-1(n≥2)
可知:an=
-
=
=
(n≥2)又a1=
满足an=
(n≥2)
故数列{ an}的通项公式an=
(n∈N*)
(2)∵an=
,则
=n(n+1)=n2+n 于是{
}的前n项之和Tn=
+
+…+
=(1+2+3+…+n)+(12+22+32+…+n2)
=
+
=
.
数列{
}的前n项和Tn:
.
| n |
| n+1 |
| 1 |
| 2 |
可知:an=
| n |
| n+1 |
| n-1 |
| n |
| n2-(n2-1) |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| n(n+1) |
故数列{ an}的通项公式an=
| 1 |
| n(n+1) |
(2)∵an=
| 1 |
| n(n+1) |
| 1 |
| an |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
=(1+2+3+…+n)+(12+22+32+…+n2)
=
| n(n+1) |
| 2 |
| n(n+1)(2n+1) |
| 6 |
| n(n+1)(n+2) |
| 3 |
数列{
| 1 |
| an |
| n(n+1)(n+2) |
| 3 |
点评:本题考查等差数列的前n项和,考查分类讨论思想与分组求和的方法,属于中档题.

练习册系列答案
相关题目
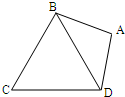 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=