题目内容
已知数列 ,设
,设 ,数列{cn}满足cn=an•bn(1)求证:{bn}是等差数列;(2)求数列{cn}的前n项和Sn.
,数列{cn}满足cn=an•bn(1)求证:{bn}是等差数列;(2)求数列{cn}的前n项和Sn.
解:(1)由题意知,
∵
∴
∴数列{bn}是首项b1=1,公差d=3的等差数列(7分)
(2)由(1)知,
∴
∴ ,
,
于是
两式相减得 =
=
∴ (14分)
(14分)
分析:(1)由题意知, ,所以数列{bn}是首项b1=1,公差d=3的等差数列.
,所以数列{bn}是首项b1=1,公差d=3的等差数列.
(2)由题设条件知, ,运用错位相减法可求出数列{cn}的前n项和Sn.
,运用错位相减法可求出数列{cn}的前n项和Sn.
点评:本题考查数列的性质和应用,解题时要认真审题,注意错位相减法的应用,仔细解答.

∵

∴

∴数列{bn}是首项b1=1,公差d=3的等差数列(7分)
(2)由(1)知,

∴

∴
 ,
,于是

两式相减得
 =
=
∴
 (14分)
(14分)分析:(1)由题意知,
 ,所以数列{bn}是首项b1=1,公差d=3的等差数列.
,所以数列{bn}是首项b1=1,公差d=3的等差数列.(2)由题设条件知,
 ,运用错位相减法可求出数列{cn}的前n项和Sn.
,运用错位相减法可求出数列{cn}的前n项和Sn.点评:本题考查数列的性质和应用,解题时要认真审题,注意错位相减法的应用,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,设
,设 ,数列
,数列 。
。
 ,设
,设 ,数列
,数列 .
.  是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围. ,设
,设 ,数列
,数列 。
。
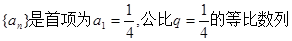 ,设
,设 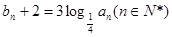 ,数列
,数列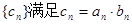 。
。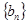 是等差数列;
(2)求数列
是等差数列;
(2)求数列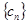 的前
的前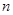 项和
项和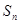 ;
;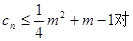 一切正整数
一切正整数