题目内容
已知数列![]() ,设
,设![]() ,数列
,数列![]() 。
。
(1)求证:![]() 是等差数列;
是等差数列;
(2)求数列![]() 的前n项和Sn;
的前n项和Sn;
(3)若![]() 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
(2)![]() 、
、 ![]()
(3)![]()
解析:
(1)由题意知,![]()
![]()
![]()
∴数列![]() 的等差数列……………………………………3分
的等差数列……………………………………3分
(2)由(1)知,![]()
![]() …………………………………… 4分
…………………………………… 4分
![]()
于是![]()
两式相减得![]()
![]()
![]() ……………………………………8分
……………………………………8分
(3)![]()
![]()
∴当n=1时,![]()
当![]() ∴当n=1时,
∴当n=1时,![]() 取最大值是
取最大值是![]()
又![]()
![]()
即![]() …………………………………… 12分
…………………………………… 12分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ,设
,设 ,数列
,数列 。
。
 ,设
,设 ,数列
,数列 .
.  是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围. ,设
,设 ,数列
,数列 。
。
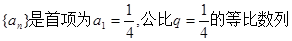 ,设
,设 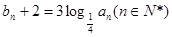 ,数列
,数列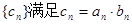 。
。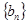 是等差数列;
(2)求数列
是等差数列;
(2)求数列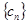 的前
的前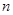 项和
项和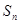 ;
;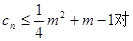 一切正整数
一切正整数