题目内容
 已知椭圆C:
已知椭圆C: 的离心率
的离心率 ,且右焦点F到左准线的距离为3.
,且右焦点F到左准线的距离为3.
(1)求椭圆C的方程;
(2)又已知点A为抛物线y2=2px(p>0)上一点,直线FA与椭圆C的交点B在y轴的左侧,且满足 ,求p的最大值.
,求p的最大值.
解:(1)∵ 的离心率
的离心率 ,∴
,∴ .①
.①
而右焦点到左准线的距离d= .②
.②
由①②解得a= ,c=1,从而b=1.
,c=1,从而b=1.
从而所求椭圆方程为 (6分)
(6分)
(2)椭圆的右焦点为F(1,0),点B在椭圆 (x<0)上.
(x<0)上.
设B(x0,y0),其中 ,
,
由 ,知
,知 ,
, .
.
由点A在抛物线y2=2px上,得 .
.
又 ,∴
,∴ .令t=x0+2,则
.令t=x0+2,则 .
.
即 .
.
∵ ,
,
∴ (当且仅当
(当且仅当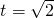 时取“=”).
时取“=”).
∴ .
.
又当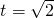 时,
时, 为椭圆在y轴左侧上的点.
为椭圆在y轴左侧上的点.
故p的最大值为 .(14分)
.(14分)
分析:(1)首先由离心率得出 ,然后根据右焦点到左准线的距离d=
,然后根据右焦点到左准线的距离d= ,就可以求出椭圆方程;
,就可以求出椭圆方程;
(2)先设B点坐标,然后根据 ,表示出A点坐标,并代入抛物线方程得出
,表示出A点坐标,并代入抛物线方程得出 ,再令t=x0+2,用的含p式子表示p,
,再令t=x0+2,用的含p式子表示p,
点评:本题考查了椭圆的简单性质以及椭圆与抛物线的综合,巧用a+b≥2 是解决(2)问的关键,属于中档题.
是解决(2)问的关键,属于中档题.
 的离心率
的离心率 ,∴
,∴ .①
.①而右焦点到左准线的距离d=
 .②
.②由①②解得a=
 ,c=1,从而b=1.
,c=1,从而b=1.从而所求椭圆方程为
 (6分)
(6分)(2)椭圆的右焦点为F(1,0),点B在椭圆
 (x<0)上.
(x<0)上.设B(x0,y0),其中
 ,
,由
 ,知
,知 ,
, .
.由点A在抛物线y2=2px上,得
 .
.又
 ,∴
,∴ .令t=x0+2,则
.令t=x0+2,则 .
.即
 .
.∵
 ,
,∴
 (当且仅当
(当且仅当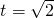 时取“=”).
时取“=”).∴
 .
.又当
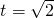 时,
时, 为椭圆在y轴左侧上的点.
为椭圆在y轴左侧上的点.故p的最大值为
 .(14分)
.(14分)分析:(1)首先由离心率得出
 ,然后根据右焦点到左准线的距离d=
,然后根据右焦点到左准线的距离d= ,就可以求出椭圆方程;
,就可以求出椭圆方程;(2)先设B点坐标,然后根据
 ,表示出A点坐标,并代入抛物线方程得出
,表示出A点坐标,并代入抛物线方程得出 ,再令t=x0+2,用的含p式子表示p,
,再令t=x0+2,用的含p式子表示p,点评:本题考查了椭圆的简单性质以及椭圆与抛物线的综合,巧用a+b≥2
 是解决(2)问的关键,属于中档题.
是解决(2)问的关键,属于中档题. 
练习册系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、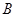 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.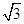
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线