Question

【题目】函数是上的奇函数，当时，.

（1）求的解析式并画出函数的图像；

（2）求的根的个数.

Answer 1

【答案】（1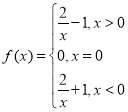）；图像见详解；（2）见详解.

【解析】

（1）由，得，根据已知解析式，得到，再由函数是奇函数，即可得出解析式；根据解析式作出图像即可；

（2）由（1）的图像，得到与直线交点个数的情况，再由方程的根的个数，即是与直线的交点个数，即可得出结果.

（1）若，则，因为当时，，

所以，

又函数是上的奇函数，所以，因此；

易知，

所以；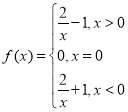

画出其图像如下：

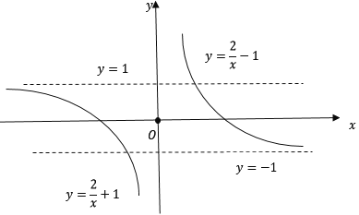
（2）由（1）中图像可得：当或时，与直线有一个交点；

当或时，与直线有两个交点；

当时，与直线有三个交点；

因为方程的根的个数，即是与直线的交点个数，

因此，当或时，的根的个数为个；

当或时，的根的个数为个；

当时，的根的个数为个；