题目内容
(13分)设二次函数 的图像过原点,
的图像过原点,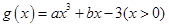 ,
,
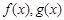 的导函数为
的导函数为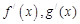 ,且
,且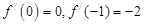 ,
,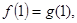
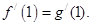
(1)求函数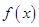 ,
,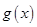 的解析式;(2)求
的解析式;(2)求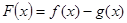 的极小值;
的极小值;
(3)是否存在实常数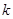 和
和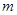 ,使得
,使得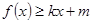 和
和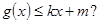 若存在,求出
若存在,求出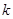 和
和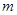 的值;若不存在,说明理由。
的值;若不存在,说明理由。
【答案】
解 :(1)由已知得 ,
,
则 ,从而
,从而 ,∴
,∴
 ,
, 。
。
由
 得
得 ,解得
,解得
 。……………………4分
。……………………4分
(2) ,
,
求导数得 。……………………8分
。……………………8分

 在(0,1)单调递减,在(1,+
在(0,1)单调递减,在(1,+ )单调递增,从而
)单调递增,从而 的极小值为
的极小值为 。
。
(3)因  与
与 有一个公共点(1,1),而函数
有一个公共点(1,1),而函数 在点(1,1)的切线方程为
在点(1,1)的切线方程为 。
。
下面验证 都成立即可。
都成立即可。
由  ,得
,得 ,知
,知 恒成立。
恒成立。
设 ,即
,即  ,
,
求导数得 ,
,
 在(0,1)上单调递增,在
在(0,1)上单调递增,在 上单调递减,所以
上单调递减,所以
 的最大值为
的最大值为 ,所以
,所以 恒成立。
恒成立。
故存在这样的实常数 和
和 ,且
,且
 。……………………13分
。……………………13分
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
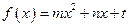 的图像过原点,
的图像过原点,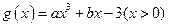 ,
,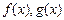 的导函数为
的导函数为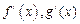 ,且
,且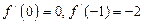 ,
,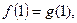
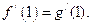
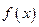 ,
,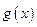 的解析式;(2)求
的解析式;(2)求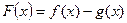 的极小值;
的极小值;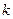 和
和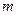 ,使得
,使得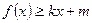 和
和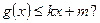 若存在,求出
若存在,求出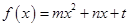 的图像过原点,
的图像过原点,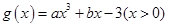 ,
,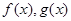 的导函数为
的导函数为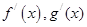 ,且
,且 ,
,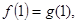
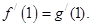
 ,
,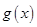 的解析式;
的解析式;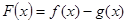 的极小值;
的极小值;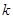 和
和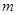 ,使得
,使得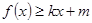 和
和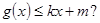 若存在,求出
若存在,求出 的图像过原点,
的图像过原点, ,
, 的导函数为
的导函数为 ,且
,且 ,
,

 ,
, 的解析式;
的解析式; 的极小值;
的极小值;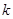 和
和 ,使得
,使得 和
和 若存在,求出
若存在,求出