题目内容
![]() -1的直线与抛物线
-1的直线与抛物线![]() 交于两点A,B,如果
交于两点A,B,如果![]() (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。
p=2.;抛物线方程为y2=4x,焦点坐标为F(1,0).
解析:
直线方程为y=-x+4,联立方程![]() ,消去y得,
,消去y得,![]() .
.
设A(![]() ),B(
),B(![]() ),得
),得![]()
所以:![]() ,p>0.
,p>0.
由已知![]() 可得
可得![]() +
+![]() =0,从而16-8p=0,得p=2.
=0,从而16-8p=0,得p=2.
所以抛物线方程为y2=4x,焦点坐标为F(1,0).

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
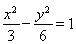
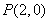
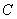
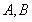
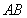
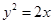 ,过动点
,过动点 且斜率为1的直线
且斜率为1的直线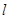 与抛物线交于不同两点A、B,|AB|
与抛物线交于不同两点A、B,|AB|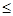 2.
2.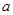 的取值范围;
的取值范围;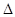 NAB面积的最大值.
NAB面积的最大值. 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线 的右焦点重合,过点
的右焦点重合,过点 且斜率为1的直线
且斜率为1的直线 与抛物线
与抛物线 两点
两点 中点到抛物线准线的距离
中点到抛物线准线的距离 交于两点A,B,如果
交于两点A,B,如果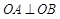 (O为原点)求P的值及抛物线的焦点坐标.
(O为原点)求P的值及抛物线的焦点坐标.