题目内容
如图四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上,O为AC与BD的交点.
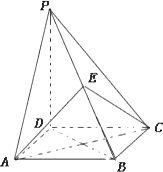
(1)求证:平面![]() ;
;
(2)当E为PB中点时,求证:OE∥平面PDA,OE∥平面PDC.
(3)当![]() 且E为PB的中点时,求AE与平面PBC所成的角的大小.
且E为PB的中点时,求AE与平面PBC所成的角的大小.
答案:
解析:
解析:
|
(1)∵四边形ABCD是正方形,∴AC⊥BD, ∵ ∴PD⊥AC, ∴AC⊥平面PDB, 又 ∴平面 (2)∵四边形ABCD是正方形, (3)∵ 所以,可以D为坐标原点建立如图的空间直角坐标系D-xyz.设AB=1.则 D(0,0,0),A(1,0,0),C(0,1,0),B(1,1,0),P(0,0, 从而, 设平面PBC的一个法向量为 令z=1,得 |

练习册系列答案
相关题目
 得
得

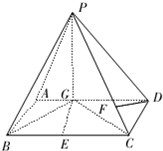 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且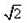 ,F是BC的中点.
,F是BC的中点.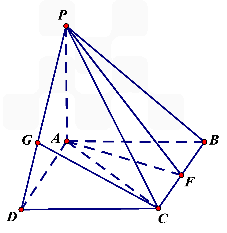
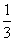 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.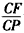 的值。
的值。 
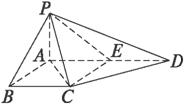
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.