题目内容
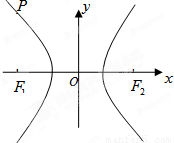
双曲线E经过点P(-4,6),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=2.
(Ⅰ)求双曲线E的方程;
(Ⅱ)求∠F1PF2的角平分线所在直线的方程.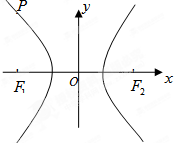
(Ⅰ)求双曲线E的方程;
(Ⅱ)求∠F1PF2的角平分线所在直线的方程.

依题意,可设双曲线方程为
-
=1,(a>0,b>0),c2=a2+b2(c>0)
(Ⅰ)∵双曲线E经过点P(-4,6),离心率e=2,
∴
-
=1,
=4
∴a2=4,b2=12
∴E的方程为
-
=1
(Ⅱ)由(Ⅰ)知,c=4,设F1(-4,0),F2(4,0),
∵P(-4,6),∴PF1⊥x轴
设∠F1PF2的角平分线交x轴于点M(m,0)
由角平分线的性质可知
=
,即
=
,∴m=1
∴M(1,0)
故所求直线方程为y=
(x-1),即6x+5y-6=0.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)∵双曲线E经过点P(-4,6),离心率e=2,
∴
| 16 |
| a2 |
| 36 |
| b2 |
| a2+b2 |
| a2 |
∴a2=4,b2=12
∴E的方程为
| x2 |
| 4 |
| y2 |
| 12 |
(Ⅱ)由(Ⅰ)知,c=4,设F1(-4,0),F2(4,0),
∵P(-4,6),∴PF1⊥x轴
设∠F1PF2的角平分线交x轴于点M(m,0)
由角平分线的性质可知
| |F1M| |
| |MF2| |
| |PF1| |
| |PF2| |
| m+4 |
| 4-m |
| 10 |
| 6 |
∴M(1,0)
故所求直线方程为y=
| 6-0 |
| -4-1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
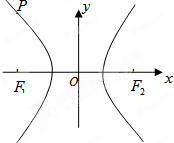 双曲线E经过点P(-4,6),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=2.
双曲线E经过点P(-4,6),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=2.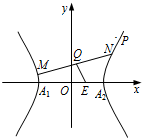 如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为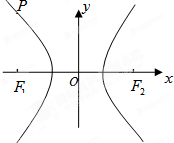 双曲线E经过点P(-4,6),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=2.
双曲线E经过点P(-4,6),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=2.